二項定理

二項定理

田邑麻呂 さんの書込 (2006/06/21(Wed) 20:52)

はじめまして，大学１年のタムラマロです．

数学で分からないことがあります．

(a+b)^(2)=a^2 + 2ab + b^2は，周知の通りですが・・・

(a+b)^(1/2)の分解はどのような形になるのでしょうか？？

教えてください．

Re: 二項定理

Chappy さんのレス (2006/06/21(Wed) 23:01)

はじめまして，Chappyというものです．

テイラー展開をご存知なら，それを利用してみるのはどうでしょうか？ 一年生で微分積分の講義を取っていると， テイラー展開を教わると思います． それとも，まだ教わってないですかね？？

Re: 二項定理

Chappy さんのレス (2006/06/21(Wed) 23:43)

追記です．．． テイラー展開をご存じないかもしれないので， 展開した結果だけを書いておきます． \alpha は任意の実数として，

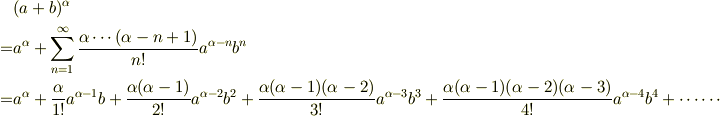
&(a+b)^\alpha \\=&a^\alpha+\sum_{n=1}^{\infty}\frac{\alpha\cdots(\alpha-n+1)}{n!}a^{\alpha-n}b^n \\=&a^\alpha+\frac{\alpha}{1!}a^{\alpha-1}b+\frac{\alpha(\alpha-1)}{2!}a^{\alpha-2}b^2 +\frac{\alpha(\alpha-1)(\alpha-2)}{3!}a^{\alpha-3}b^3+\frac{\alpha(\alpha-1)(\alpha-2)(\alpha-3)}{4!}a^{\alpha-4}b^4+\cdots\cdots

（上の式がちゃんと意味を持つには少し条件が要ります）

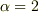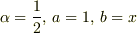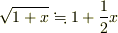いかがですか？ ３番目の式に \alpha=2 を入れてみてください． おなじみの式が出てきます． \alpha=\frac{1}{2},\,a=1,\,b=x を代入して，第３項以下を無視すると， 高校の物理でよく出る近似式 \sqrt{1+x}\fallingdotseq 1+\frac{1}{2}x が現われます．

Re: 二項定理

田邑麻呂 さんのレス (2006/06/23(Fri) 13:01)

Chappyさんありがとうございました．

やはりテイラー展開の近似手法が一般的なんですね．