定積分

home > 掲示板 >

このページのPDF版

サイトマップ

定積分

PHYSIC さんの書込 (2006/06/19(Mon) 21:46)

はじめまして．

{Ze^{2}/4πε}∫{b/b^{2}+v^{2}t}dt

を解くと

Ze^{2}/2πεbv

と，なるはずなんですが，解けません．積分は定積分で，範囲は−∞＜t＜∞です．

積分部の分母を文字で置いて解けるかと思いましたが，積分部の解が０になってしまいます・・・何か良い回答方法はありませんか？よろしくお願いします．

Re: 定積分

Chappy さんのレス (2006/06/19(Mon) 23:44)

はじめまして，Chappyというものです．

早速，質問に関してですが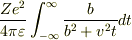， $\frac{Ze^2}{4\pi\varepsilon}\int_{-\infty}^{\infty}\frac{b}{b^2+v^2t}dt$ 問題はこれでよろしいですか？もしかしたら，はに依存していたりしませんか？問題がこれでよければ，がんばってみます．間違ってたら教えてください．とはいっても，僕が解ける保証はありません，ごめんなさい，，，まぁ，他の優秀な方が解いてくれるかもしれませんし，落胆しないで下さいね．

Re: 定積分

PHYSIC さんのレス (2006/06/20(Tue) 00:26)

Chappyさん．はじめまして〜問題が見づらくて申し訳ありません＾＾；

問題は全くもってその通りです．

ｖがｔに依存しているかどうかははっきりとは分かりませんが，多分依存していないんじゃないかなと思います．

私もいま参考書なんかを漁って解法を探してるんですけど未だに見つかりません；；どうかお助けください！

Re: 定積分

Chappy さんのレス (2006/06/20(Tue) 01:02)

依存してなかったら，次のように計算できると思います．間違った方向に行ってしまったようなので，全部載せちゃいます．

$&\frac{Ze^2}{4\pi\varepsilon}\int_{-\infty}^{\infty}\frac{b}{b^2+v^2t}dt \\=&\frac{Ze^2}{4\pi\varepsilon}\lim_{n \to \infty}\left[\frac{b}{v^2}\log|b^2+v^2t|\right]_{-n}^{n} \\=&\frac{Ze^2}{4\pi\varepsilon}\lim_{n \to \infty}\frac{b}{v^2}\log\left|\frac{b^2+v^2n}{b^2-v^2n}\right| \\=&0$

となってしまう気がします・・・・・僕もだめでした，ごめんなさい，，，(^_^; 計算方法違ってたら，教えてくださいね．しかし，どうしたものか・・・・・・

Re: 定積分

toorisugari no Hiro さんのレス (2006/06/20(Tue) 01:14)

積分そのものから間違っている気がします．完全な問題を載せてください．

Re: 定積分

PHYSIC さんのレス (2006/06/20(Tue) 07:05)

あ〜！！すみません！！積分部分の分母が二分の三乗でくくってありました．

[b^2+v^(2)t]^(3/2)

ですけど，やはり０になるような気がします・・・どうすればいいですかね・・・

Re: 定積分

Joh さんのレス (2006/06/20(Tue) 08:11)

変数の物理的な意味は何もないんですか？（単なる積分の練習問題なのですか？）

Re: 定積分

toorisugari no Hiro さんのレス (2006/06/20(Tue) 13:52)

> どうすればいいですかね・・・

完全な問題をみせてください．

Re: 定積分

Chappy さんのレス (2006/06/21(Wed) 00:17)

問題の数式見る限り，物理の問題っぽいですねぇ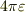．．． $4\pi\varepsilon$ が意味深長です． toorisugari no Hiro さんのおっしゃるとおり，式の導出の段階で間違ってしまったのかもしれませんね．問題の最初から考えてけば，間違った箇所が見つかるかもしれませんよ？

Re: 定積分

mNeji さんのレス (2006/06/21(Wed) 03:25)

頭の体操と思って眺めます：

ざっとみると，電場か電場ポテンシャルかを出そうとしている感じですね．

そこで積分範囲，−∞から+∞，を 0から+∞ にすると，

int_0^(+∞) {(b)/(b^2 + v^2)^(3/2)}dt =2v^{-2}

となるような気もしますが...．

Re: 定積分

ｙama さんのレス (2006/06/21(Wed) 16:18)

[b^2+v^(2)t]^(3/2) は t<-(b/v)^2 のとき虚数になってしまうので，積分範囲が−∞から+∞というのはおかしいように思います．被積分関数か積分範囲かどちらかが間違っているような気がします．

Re: 定積分

神谷さんのレス (2006/06/22(Thu) 03:10)

初めまして．神谷と申します．大学で積分の勉強をしたことはありませんが，敢えて申し上げさせていただきます．積分部分の括弧内のtの羃はひょっとしたら1ではなく2ではないでしょうか？もしそうであるならば，すんなりと積分出来てしまうのですが…

Re: 定積分

Chappy さんのレス (2006/06/22(Thu) 17:28)

はじめまして，神谷さん．僕はChappyというものです．

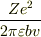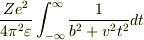
なるほど，確かに，積分がうまくいきますね．こうなると，少し係数を変えれば答えの式 $\frac{Ze^2}{2\pi\varepsilon bv}$ に合わすことができそうです．次の積分なんかはどうでしょう．係数が分からないから怪しいものですが．．． $\frac{Ze^2}{4{\pi}^2\varepsilon}\int_{-\infty}^{\infty}\frac{1}{b^2+v^2t^2}dt$

Re: 定積分

なんとなくさんのレス (2006/06/22(Thu) 18:38)

こんにちは．

なんか良く見る式なので，一言．この式形はｂを衝突パラメータ(impact paremeter)，ｖを入社粒子の速度としたときの散乱計算ですね．ただ，被積分部分で何をしているか決まるので，3/2乗なら，総エネルギー変化かなんかっぽい気がします．やはり，正確な式が必要ですね．

Re: 定積分

神谷さんのレス (2006/06/22(Thu) 18:42)

どうも(^^ ) 私の計算があたってるかどうか自信は無いのですが，chappyさんがお出しになった積分も当初の積分(括弧内のtの羃が2)の計算結果と同じではないかと思います．

Re: 定積分

ｙama さんのレス (2006/06/29(Thu) 11:40)

結局神谷さんのおっしゃる通り，次のようになるのでしょうね． $\frac{Ze^2}{4\pi\epsilon}\int_{-\infty}^{\infty}\frac{b}{(b^2+v^2t^2)^{\frac{3}{2}}}dt=\frac{Ze^2}{4\pi\epsilon}\left[\frac{t}{b\sqrt{b^2+v^2t^2}}\right]^{\infty}_{-\infty}=\frac{Ze^2}{2\pi\epsilon bv}$ これだと，物理的な意味も別記事（角速度）に書いたように考えることができるし・・・．

[home] [掲示板] [ページの先頭]