POTYOMUKIN さんの書込 (2006/06/18(Sun) 18:51)

どうもはじめまして． 質点が，鉛直面内にある滑らかなサイクロイド：ｘ＝a（θ＋sinθ） ｙ＝a（１−cosθ） の上に束縛されていて，重力の作用の下に運動するとき，その周期は振幅によらないことを示せ．（ヒントはエネルギー保存の法則から，弧の長さs=4asin(θ/2)についての単振動の方程式を導け．） という問題ですが， 0からθの積分でｓを求めたのですが，これってエネルギー保存で求めてませんよね多分？他に方法があるのでしょうか？ それとこのあと運動方程式でθ/２＝θ’とおいて接線方向の力を−mgsinθ’とおいて解いたのですが，θ/２＝θ’とおくこの行動はありでしょうか？なしの場合運動方程式とsinθをどう求めたらよいのでしょうか？[cosθ＝1−2sin^2（θ）を使ったのですがsinθ＝s/8a(s^2-16a^2)^(1/2)になってしまいちょっとうまくいかないのです．] どなたかよろしくお願いします．

yama さんのレス (2006/06/18(Sun) 20:19)

s についての運動方程式をつくればいいのです． つまり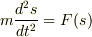， の形の方程式を導くわけです．

POTYOMUKIN さんのレス (2006/06/18(Sun) 20:59)

返信ありがとうございます． ちょっと詳しくいってなかったので 0からθの積分でｓを求めs=4asin(θ/2)がでたんですね．これがエネルギー保存で求めてないのかなというのが一つ目の疑問で． そのあと θ/２＝θ’とおいて接線方向の力を−mgsinθ’としてs=4asin(θ/2)からsinθ’＝sin(θ/2)=s/4a 運動方程式ｍd^2s/dt^2=-−mgsinθ’＝-mgs/4a d^2s/dt^2＝-gs/4aから T=2π（4a/g)^(1/2)となり周期は振幅によらないとしたのですが，θ/２＝θ’とおくこの行動はありでしょうか？というのが二つ目の疑問です．そしてだめの場合どうすればいいのかということでした． よろしくお願いします．

なんとなく さんのレス (2006/06/18(Sun) 22:47)

こんにちは．

横やりすみませんが，興味を持ったので．

POTYOMUKINさん，もうほぼ正しい答えを出されているので，こう考えたらいかがでしょう． 弧長，S=4asin(θ/2)はエネルギー保存とは関係ないですが，この問題の 全エネルギーEは，E=(1/2)md^2S/dt^2+mgy・・・? と表され，y=a(1-cos(θ))=(1/2)asin^2(θ/2)=(1/8)S^2/a^2 となります．そこで，E=(1/2)md^2S/dt^2+(mg/8)S^2/a^2・・・? ですね． これが一定（エネルギー保存）より，その微分＝０なので，?をｔで微分して， m(dS/dt)(d^2S/dt^2)+(mg/4)(dS/dt)S/a^2=0 つまり， d^S/dt^2+(g/4a^2)S=0 というおなじみ，単振動の方程式が出てくるわけですね． あとは，どこがどう違うか，もうお分かりでしょう．

yama さんのレス (2006/06/18(Sun) 23:09)

エネルギーの保存を利用する方法は，なんとなくさんが説明された通りです．

POTYOMUKINさんの方法でも運動方程式は導けます． この場合は，接線方向の力の成分が 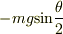になることを用いていますね．確かにそうなるのですが，そのことをきちんと示すことができますか？

POTYOMUKIN さんのレス (2006/06/19(Mon) 00:21)

なんとなくさん＜返信ありがとうございます．じっくりと考えてみたいと思います．

yamaさん＜返信ありがとうございます．−mgsin(θ/2)をきちんと示すことができますかということですが，自分はホントは−mgsinθとなるのかなとおもってたのですが，s=4asin(θ/2)とθ/2がでたので，どうせ周期にθは入らなくなるのでθ/２＝θ’とおきました（むちゃくちゃかもしれませんが）．結局の所なぜかは分かりません．しばらく考えてみましたが検討がつきませんでしたすみません．

yama さんのレス (2006/06/19(Mon) 07:29)

θはサイクロイドを表すパラメータであって，接線の傾きの角度ではないので，重力の接線方向の成分は-mgsinθ ではありません． 接線の傾きの角度をθ’とすると，重力の接線方向の成分は-mgsinθ’になりますね． θ’とθの関係については，tanθ’=dy/dx=tan(θ/2) すなわち θ’=θ/2 になることが分かります．計算して確かめてください．

ところで，見落としていましたが，なんとなくさんが書かれた?式および?式の中の d^2S/dt^2 は (dS/dt)^2 の書き間違いだと思いますが・・・．

POTYOMUKIN さんのレス (2006/06/19(Mon) 16:06)

なるほどそういうことだったんですね． わかりました．計算してみます． ありがとうございました．

なんとなく さんのレス (2006/06/19(Mon) 20:53)

>yamaさん，こんにちは．

ありゃりゃ，速度の２乗ですから，そのとおりです． どう間違っているか，自分で分かりませんでした(^o^;)． 御指摘ありがとうございます．