カリプソ さんの書込 (2006/06/18(Sun) 18:07)

惑星の運動についてのノートを読み返していたら，知らない用語が出てきました．「中心力量」と「ニュートン場」です．辞書などで調べてみたのですがわかりませんでした．宜しくお願いします．

yama さんのレス (2006/06/18(Sun) 20:36)

「ニュートン場」とは万有引力の場のことで，ニュートンの万有引力の法則が成り立ちます． 「中心力量」という用語は初めて見ましたが，私も意味がわかりません．ひょっとするとノートの写し間違いかとも思いますが・・・どんな文脈で出てくるのか，その部分を引用していただけると何か分かるかもしれません．

カリプソ さんのレス (2006/06/19(Mon) 02:36)

x=rcosθ, y=rsinθ v_x=dr/dt cosθ - rdθ/dt sinθ, v_y=dr/dt sinθ + rdθ/dtcosθ v_r=v_xcosθ + v_ysinθ=dr/dt, v_θ=-v_xsinθ + v_ycosθ=r dθ/dt a_x=d^2r/dt^2 cosx - 2 dr/dt dθ/dt sinθ-r d^2θ/dt^2cosθ - r (dθ/dt)^2cosθ, a_y=d^2r/dt^2 sinθ + 2 dr/dt dθ/dt cosθ + r d^2θ/dt^2cosθ -r(dθ/dt^2)^2sinθ a_r=a_xcosθ + a_ysinθ=d^2r/dt^2-r(d^2θ/dt^2)^2 , a_θ=-a_xsinθ + a_ycosθ=rd^2θ/dt^2 + 2dr/dt d^2θ/t^2 d(r^2 dθ/dt)/dt=ra_θ＝０（角運動量保存） よってa_θ=0 a_θ：中心力量

読みにくいと思いますが宜しくお願いします．

mNeji さんのレス (2006/06/19(Mon) 04:45)

私は，関節とリンクのモデル計算を準備中のものです．

上記の式は，モデル計算を表示するためのASCIImathML.jsの式ソースに類似しているので，書いて見ました．

• http://www.as-ia.co.jp/ykwk/wiki.cgi?test%2feq_of_motion

回転運動を極座標にして表示しているようですね．

質量mでも補えば，

｛（慣性能率*角速度)＝角運動量｝の時間微分 ＝トルク

の式と見えます．

a_θは，角度方向の加速度では？

ｙama さんのレス (2006/06/19(Mon) 11:06)

平面極座標での加速度成分を求める計算ですね． ｍNejiさんのおっしゃる通り，a_θ は，角度方向（円周方向）の加速度成分，a_r は半径方向の加速度成分です． a_θ を中心力量とは普通は言わないと思います．何かの間違いではないでしょうか．

mNeji さんのレス (2006/06/19(Mon) 11:47)

ｙamaさん，補足ありがとうございます．

>角度方向（円周方向）の加速度成分

超久しぶりだったので，計算方法は覚えていても,用語が出てこなくて...．

カリプソ さんのレス (2006/06/19(Mon) 14:59)

mNejiさん，yamaさん，返事ありがとうございます．友達のノートと比べてみて確認して，また報告させていただきます．計算過程も少し不安が残るのでまた疑問ができた時はよろしくお願いします．

トンガリ さんのレス (2006/06/20(Tue) 15:51)

私は，工業用ミシン(6,000rpm)の天秤と呼ぶ四節リンク機構の運動解析で，40年前に入社直後， 平面極座標での加速度成分などの式を天秤に応用したドイツ語の文献を業務で翻訳させられた． しかし，設計や自他社製品の比較評価に用いるFORTRANでの計算には，これ等の式を使わなかった．

【私が使った方法】 １．天秤の二個のリンク部品と一個のクランクピンの質量と重心の位置は現物を計測して得た． ２．四節リンク機構のリンクの運動は，幾何寸法に従って三角関数や余弦定理を使って一意的に求まる． ３．機構の目的である糸穴と呼ぶ最も運動の激しい部分の運動軌跡Ｘ(θ)，Ｙ(θ)，θ＝0,1,2,・・・360度も求まる． ４．Ｘ(θ)，Ｙ(θ)を各々10次まで調和解析した．そして，Ｘ(θ)，Ｙ(θ)の7次までのフーリエ合成の式を得た． ５．フーリエ合成の式を2回微分して，Ｘ(θ)，Ｙ(θ)の加速度を得て，ベクトル合成で最大加速度は1000Ｇを超えた． ６．四節リンク機構に隣接する針棒と呼ぶピストン-クランク機構の二個の部品と一個のクランクピン質量を含めて， 合計六個の質量の運動軌跡から，総重心の運動軌跡を求め，それを調和解析して， 1次のフーリエ係数四個をベクトル合成して，180度反対向に，その値の1／2のバランスウエイトを設けた． 【注意】半振幅Ｒの単絃振動は，長さＲ／2の時計回りと反時計回りに等速回転する二つの位置ベクトルの合成

であるから，バランスウエイトで相殺でき得るのは，この内の一方のみであることを考慮すること．

【参考】リサージュ曲線(t)は調和解析して，時計回りと反時計回りに等速回転する位置ベクトルの合成で表現できる．

針端が略正方形を描く機構は，X-Y座標の原点回りの四角形を調和解析して，遊星歯車機構で設計できる． 昔，遊星歯車機構に代えてスチールベルト＆プーリーの機構で直線記録のペン式記録計が外国製であった．

７．水平送り機構と呼ばれる四節リンク機構が二組直列で略直角に繋がっていて繋がった共用の一個のリンクの静止端を 手動クランクで支えてバネ力で一方向に付勢しておき，手動レバーでバネ力に抗して動かす，縫い目の自動バック機構． これは昔のコンピュータの機械式カードパンチ機構に一部似た機構で，商品仕様の水平送り量を確保しつつ， 指が疲れない．バネ力が弱くても手動レバーが振動しない．水平送り機構から発生する騒音を少なくする目的で， 水平送り運動の高次成分を極力少なくするリンク配置の探索結果の評価にも．運動の調和解析を用いた．

40年前の機械力学の教科書には，『単シリンダ機関のピストン-クランク機構における不釣り合い力とバランスウエイト』 が記載されているが，解析的でクランクロッドの質量分配に仮想クランクを使い，運動軌跡の近似式も使って苦労している．

上記の【私が使った方法】は設計・計算の方法の一提案として，いかがでしょうか．

カリプソ さんのレス (2006/06/21(Wed) 17:14)

申し訳ありません．中心力量という単語はないようです．ノートのとり間違いでした．どうもお騒がせいたしました．

No.9893での計算の中で，v_x=dr/dt cosθ - rdθ/dt sinθ, v_y=dr/dt sinθ + rdθ/dtcosθ ⇒ v_r=v_xcosθ + v_ysinθ=dr/dt ⇒ v_θ=-v_xsinθ + v_ycosθ=r dθ/dt という式変形がそもそも理解できていませんでした．どなたかご指導お願いします．

トンガリさん，返事ありがとうございます．まだ取りかかっていませんが，参考にさせていただきます．もし途中で躓いた場合また質問させていただきますので，宜しくお願いいたします．

yama さんのレス (2006/06/21(Wed) 23:28)

ある瞬間の物体の位置を原点O'とし，極座標の半径方向にx'軸，円周方向にy'軸をとった座標系を考えると，x'方向の速度成分がv_r，y'方向の速度成分がv_θになります． ところが，O'x'y'座標系はOxy座標系の原点をずらしてから，角度θだけ回転させたものです．原点のずれは，速度の成分には影響しませんが，回転は速度成分を変えます． すなわち，座標系の回転によってベクトルの成分は座標と同じように変換します． 座標の変換はx'=xcosθ +ysinθ，y'=-xsinθ + ycosθ と表されるので，(x'，y')を(v_r，v_θ)で，(x，y)を(v_x，v_y)で置き換えれば速度成分の変換を表す式になります．

mNeji さんのレス (2006/06/24(Sat) 14:27)

>No.9893での計算の中で，v_x=dr/dt cosθ - rdθ/dt sinθ, v_y=dr/dt sinθ + rdθ/dtcosθ >⇒ v_r=v_xcosθ + v_ysinθ=dr/dt >⇒ v_θ=-v_xsinθ + v_ycosθ=r dθ/dt >という式変形がそもそも理解できていませんでした．どなたかご指導お願いします．

以前計算式をASCIImathML.js形式で示したページで，2次元の場合に複素数形式で検算して於いたのですが，ご連絡するのを忘れていました．2次元でも普通のベクトル計算はミスし易く嫌になりますが，複素数計算では，三角関数に煩わされず，expの微積分の時の「i」だけに注意を払えばいいので計算が楽です．

高校生では，公に使えないでしょうが，答えを先に出してから，落ち着いて三角関数を誘導すれば良いので，お勧めです．

なお，この方法で，x,y成分に戻したいばあい， ・必要なベクトルのRe(実数成分)がx成分 ・必要なベクトルのIm(虚数成分)がy成分

を使えば良いので，再検算にも有用です．

なお，この計算で出てくる，動径ベクトル，接線ベクトルで示される座標系は，非慣性系座標である事にご注意ください．

カリプソ さんのレス (2006/07/09(Sun) 18:57)

おそくなりまして・・・ ＞ところが，O'x'y'座標系はOxy座標系の原点をずらしてから，角度θだけ回転させたものです すみません．この部分がよく理解できていません．Oxy座標も極座標なのですよね？ ＞座標の変換はx'=xcosθ +ysinθ，y'=-xsinθ + ycosθ と表されるので，(x'，y')を(v_r，v_θ)で，(x，y)を(v_x，v_y)で置き換えれば速度成分の変換を表す式になります． どうしてこのような置き換えが可能なのでしょうか？ すみません，ちょっと頭がこんがらがってきました．

yama さんのレス (2006/07/09(Sun) 21:13)

Oxy座標系は普通の直角座標系（デカルト座標系）です． O'x'y'座標系は物体の位置を原点にとった局所的な直角座標系です． x'軸をその瞬間の動径方向にとっているので，速度のx'成分v_x'は，極座標の動径成分v_rに等しくなります．同様に v_y'＝v_θ になります．

次に，座標変換に伴う速度の変換を考えてみましょう． 座標軸を平行移動しただけでは速度は変化しませんが，座標軸を回転させると速度（v_x，v_y）は座標（x，y）と同じように変換します． 平行移動を無視して，座標軸の回転だけを考えると x'=xcosθ +ysinθ，y'=-xsinθ + ycosθ なので，これに伴う速度の変換は次のようになります． v_x'=v_xcosθ +v_ysinθ，v_y'=-v_xsinθ +v_ ycosθ ここで，v_x'=v_r，v_y'＝v_θ と置くと，極座標での速度成分が得られます．もちろん，ここでv_xとv_yはrとθで表されているものとします．

カリプソ さんのレス (2006/07/11(Tue) 01:38)

ありがとうございます．助かります．また引っかかってしまったので質問させて下さい． No9893で d(r^2 dθ/dt)/dt=ra_θ＝０（角運動量保存）と記述したのですが，r^2 dθ/dtが定数であることの証明として 角運動量：Ｌ＝ｒ×mdr/dt=re_r×m(dr/dt e_r , rｄθ/dt e_θ）＝ｍｒ^2dθ/dt k っとなっているのですが(dr/dt e_r , rｄθ/dt e_θ）と成分表記されている部分がよくわかりません． e_θとは半径方向の単位ベクトルなのでしょうか？

yama さんのレス (2006/07/11(Tue) 01:56)

e_rが半径方向の単位ベクトルで，e_θは円周方向の単位ベクトルです．

カリプソ さんのレス (2006/07/11(Tue) 10:20)

e_θは円周方向の単位ベクトルですよね，，，申し訳ありません，うちまちがいました． 角運動量：Ｌ=ｒ×mdr/dt=re_r×m(dr/dt e_r , rｄθ/dt e_θ） のように成分表示できるのはなぜでしょうか？

ｙama さんのレス (2006/07/12(Wed) 12:35)

その表示はちょっとおかしいですね．「,」は「+」の間違いだと思います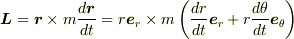． とするのが正しいと思います．

カリプソ さんのレス (2006/07/13(Thu) 01:18)

ノートのとり違いでしたか．．．ありがとうございます． （dr/dt e_r +rdθ/dt e_θ）の部分はベクトルrを微分したものということですよね？？だとすれば，r dθ/dt e_θとは何でしょうか？？e_rを微分するとdθ/dt e_θになるとことですか？

ｙama さんのレス (2006/07/13(Thu) 09:25)

カリプソさんがNo.9893で書かれているように v_r=v_xcosθ + v_ysinθ=dr/dt, v_θ=-v_xsinθ + v_ycosθ=r dθ/dt です． つまり，r dθ/dt は円周方向の速度成分 v_θ です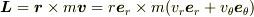． を，r や θ を用いて表したものがNo.10409の式です．

e_rを微分するとdθ/dt e_θになると考えてもかまいません．

カリプソ さんのレス (2006/07/15(Sat) 00:36)

＞e_rを微分するとdθ/dt e_θになると考えてもかまいません． この部分がよくわかりません．なぜ突然円周方向の単位ベクトルがでてくるのでしょうか？？

CO さんのレス (2006/07/15(Sat) 00:58)

カリプソさん，こんばんは．

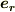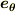， をそれぞれデカルト座標の単位ベクトル 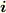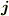， を用いて書くと，

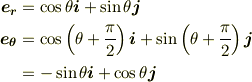
となります(図を描けばわかると思います)．ここで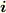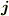， ， は時間に依存しないことに注意して下さい．

これより 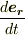を計算すると，

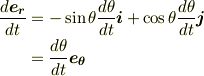
となります．