力学

力学

メモ さんの書込 (2006/06/11(Sun) 20:42)

大学，数学科の者です．物理はほとんど知りません． 問題の答案の仕方を詳しくお願いします．

問１ 速度に比例する空気による抵抗力が働く場合の自由落下の問題を考える．t=0における質点の位置をz[0]，速度v[0]として，時刻t(t≧0)における質点の位置z(t)と速度v(t)=dz(t)/dtを求めよ．ただし，質点の質量をm，重力による力を-mgおよび空気による抵抗力を-kv(t)(k＞0)とする．また，質点の運動は鉛直上方を正とするz軸上に限られるものとする．

問２ つりあいの位置からのずれをx(t)として，質量mの線形振動体を考える．復元力-kx，速度に比例する抵抗-αdx/dt(α＞0)が働く線形振動体に外力F(t)が働いている．時刻t=0における質点の位置をx[0]，速度をv[0]として，x(t)( t≧0)を求めよ．ただし，4mk＞α^2とする．

Re: 力学

toorisugari no Hiro さんのレス (2006/06/12(Mon) 12:41)

問題の丸投げはルール違反です．

問1

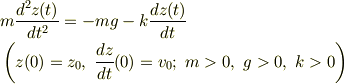
&m \frac{d^2 z(t)}{dt^2} = - m g - k \frac{d z(t)}{dt}\\&\left(z(0) = z_0,~ \frac{dz}{dt}(0) = v_0;~ m>0,~ g>0,~ k>0 \right)

という，実関数 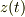z(t) に対する定数係数線形非斉次2階微分方程式の初期値問題です．あとは数学ですから自力で解いてください．

問2

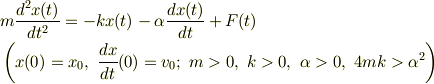
&m \frac{d^2 x(t)}{dt^2} = - k x(t) - \alpha \frac{dx(t)}{dt} + F(t)\\&\left(x(0) = x_0,~ \frac{dx}{dt}(0) = v_0;~ m>0,~ k>0,~\alpha>0,~ 4mk > \alpha^2 \right)

という，実関数 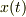x(t) に対する定数係数線形非斉次2階微分方程式の初期値問題です．あとは数学ですから自力で解いてください．

(ちょっとTeXの調子が変ですね．>管理者様) (TeXの件，うまくできました．ありがとうございました．>管理者様)

Re: 力学

CO さんのレス (2006/06/12(Mon) 14:36)

> toorisugari no Hiro さん > ちょっとTeXの調子が変ですね．>管理者様

ご報告ありがとうございます． システム側の問題でした，すみません． 現在は正常に使えるようになりました．

Re: 力学

メモ さんのレス (2006/06/13(Tue) 04:58)

ありがとうございました．