イデアルについて
イデアルについて
Chappy さんの書込 (2006/06/10(Sat) 21:26)
はじめまして,大学で数学を学んでいる学部生です. 今日はひとつ気になることができたので,ひとつ質問させてください..
代数学・イデアルの記事で,イデアルの定義が,
環  の部分環
の部分環 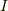 が次の性質を満たすとき,
が次の性質を満たすとき, 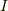 をイデアルと呼ぶ.
をイデアルと呼ぶ.
任意の 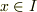 と任意の
と任意の 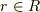 に対して,
に対して, 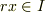 が成り立つ.
が成り立つ.
となっていましたが, 僕の持っているテキストでは,イデアルの定義が次のようになっていました.
環  の<b>部分集合</b>
の<b>部分集合</b> 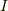 が次の性質を満たすとき,
が次の性質を満たすとき, 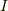 をイデアルと呼ぶ.
をイデアルと呼ぶ.
(1)任意の 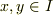 に対して,
に対して, 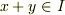 が成り立つ.
(2)任意の
が成り立つ.
(2)任意の 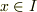 と任意の
と任意の 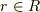 に対して,
に対して, 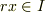 が成り立つ.
が成り立つ.
この定義は上の定義と同値でしょうか?
自分で確かめてみたところ,
結合法則が成り立っていることをどう確かめるか,というところで引っかかってしまいました.
これは,任意の 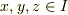 で,
で,
 の範疇で,結合法則
の範疇で,結合法則 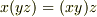 が成り立っていて,
が成り立っていて,
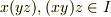 だから,
だから, 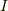 において結合法則
において結合法則 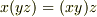 が成り立っているという考えでよろしいでしょうか?
が成り立っているという考えでよろしいでしょうか?
読みにくく長い文章で申し訳ありません. ご返事をいただけたら幸いです.
Re: イデアルについて
yama さんのレス (2006/06/10(Sat) 23:48)
それでいいと思います.
Re: イデアルについて
Chappy さんのレス (2006/06/11(Sun) 01:44)
そうですか. ご返事ありがとうございます. 安心して眠れそうです...
Re: イデアルについて
Joh さんのレス (2006/06/11(Sun) 02:13)
Chappyさん,イデアルの記事を書いたものです. 安心して眠れそうだということで,良かったです.
まだ間違いやおかしなところがあったら,掲示板か プロジェクトのメイル宛に教えて下さいね. もしよければ,一緒に数学の記事を書きませんか. (↑勧誘)
Johさんへ
Chappy さんのレス (2006/06/11(Sun) 15:18)
いやぁ,僕は代数は得意なわけじゃないです... 線形代数は得意ですが. 代数は習いたての学部3年です. 僕は幾何よりな方ですかね,最近は動標構のほうに興味があります.
Johさんの記事は,数学について書いてあるのに読みやすくて好きです. 数学の歴史など読んでいて面白いです. これからもがんばってくださいね.
関係のない話ですが,僕は中学のときに,本を見ながら, ガウスの正13角形を作図したことがあります. 作図するのは楽しく難しいものですね.