単振動
単振動
TAKA さんの書込 (2006/06/09(Fri) 22:56)
大学の物理でわからないところがあるので教えてください．
ピンと張った長さLの紐の中央に固定されている質量mの物体がある． 物体は紐から常に一定の力Sで引っ張られている． 物体を少し変位させて静かに離すと振動する． 物体の変位をxとして，そのときの物体にかかる復元力を求めよ． （鉛直上向きを正として，物体にかかる力の合力を計算する．） この復元力をxが小さいとしてTaylor展開し，単振動と近似したときの運動方程式を求めよ． この振動の周期を求めよ．
問題と少し違うやり方のとき
F≒-S*(x/(L/2))*2=-(4S/L)x T=2Π√(mL/S)
となったのですが，問題の指示通りのやり方がよく分かりません． どなたか教えていただけませんか，よろしくお願いします．
Re: 単振動
TAKA さんのレス (2006/06/10(Sat) 01:02)
F=-S*x/(√((L/2)^2+x^2)*2=4Sx/√(L^2+4x^2)
としたのですが自信がありません． 見にくくてすいません．
Re: 単振動
toorisugari no Hiro さんのレス (2006/06/10(Sat) 01:44)
たしかに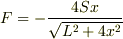 
から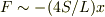 
がでますね．
# Taylor展開はおおげさなような．．．
ともかく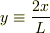 
と置き換えてから， 
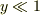を利用してTaylor展開あるいは一次関数近似をされてはどうでしょう．
