kira さんの書込 (2006/06/06(Tue) 20:01)

はじめまして．私は社会人で会社経営をしているものです．年齢は２５です．表示されている名前は会社名で，まだホームページはありません．趣味でテニスをします．ある日「テニスボールはどんなふうに動くのか？」というシュミレーションプログラムを作成してみようと思い（なぜそんな事を突然思ったかは謎・・・）とりあえず製作してみたのですが，物理の知識に乏しい私のプログラムは空気抵抗を無視したものしか作れませんでした．そのプログラムの設定は，初速をVoCos,VoSinとしたとき， x=VoCos x t y=VoSin x t - (gt^2)/2 というものでした． しかし，なんとか空気抵抗も考慮に入れたものを作りたいと思い，色々と調べた結果，「物理のがぎしっぽ」にたどり着きましたが，いまいちよくわかりませんでした．とりあえず，「微分・積分・数列・指数・対数」もよくわからなかったので，参考書等を購入して，勉強したのですが，それでも混乱するばかりでした． とりあえず，このサイト「物理のかぎしっぽ」の「力学」の「抵抗力のある落下運動」をヒントにしたいのですが，最後の「位置の式」のＣ１とＣ２が分かりません． 「位置の式」

X = -(mC1e^-kt/m)/k + mgt/k +C2

C1はVo -mg/kであってますか？C2はm(Vo-mg/k)/kであってますか？ また，X(位置)が分かっているとき，ｔ(時間)を求める式はどういう風に求めるのでしょうか．また空気抵抗ｋはテニスボールの場合どれくらいなのでしょうか？ 上の「位置の式」を「放物運動」のＸ軸に応用する場合，ｇは０でいいのでしょうか？ 最後に，この質問文の入力方法が，いまいち理解できず，式が見にくくてすみません．仕事の都合上，なかなかパソコンは利用しないので，返信等も遅れるかもしれませんが，よろしくお願いいたします．

Joh さんのレス (2006/06/06(Tue) 21:14)

いま考えていらっしゃる式とは違う話になるのですが，ボールの抵抗は一般にもっと複雑な式になると思います．ボールは回転していますし，空気の粘性を無視できないので，後ろに渦を引きます．渦によって誘起される抵抗を考えないといけないような気がします．

kmvで表わされる空気抵抗は一番簡単な一次近似ですので，十分高い高さから物を落下させた場合の終端速度を求めるような場合には役に立つと思いますが，ポンポンやりとりするテニスボールの抵抗に当てはめてどれくらい正確なものか，よく見当がつきません．

もしプログラムが出来たら，結果を教えて下さい．

kira さんのレス (2006/06/06(Tue) 22:51)

返信ありがとうございました．確かにＪｏｈさんの言う通り，今の考え方では，あまり正確ではないようですね．残念です．物理は奥が深いですね． しかし，正確ではないにせよ，今の空気抵抗を無視したプログラムよりはマシなような気がするし，解らないままだとスッキリしないので，とりあえず最初の質問のＣ１，Ｃ２及びｔ(時間)の求め方をどうにか解決したいですねぇ．

ところで話は変わります．どういう方法でホームページを作成するのか，これから勉強するところですが，創立３年目になるので，なんとか会社のホームページを来年までには作成したいと思います．そのなかに，上手にできていたらプログラムをダウンロードできるようにしておきますので，利用してみてください．

山旅人 さんのレス (2006/06/10(Sat) 17:32)

kira さんは，まだご覧になっていますでしょうか？

> X = -(mC1e^-kt/m)/k + mgt/k +C2
> C1はVo -mg/kであってますか？C2はm(Vo-mg/k)/kであってますか？ 

C1，C2 ともにあっています．ただし，ご覧になったサイト 「抵抗力のある落下運動」 は，下向き（重力方向）を正としていること，さらに C2 をこのように与える場合は，t＝0 のとき X＝0 としている，すなわち X を “落下距離” と考えている，ということにご注意ください． kira さんが考えておられる y=VoSinθ・t - (gt^2)/2 は，上向きを正としていますので注意して応用してください．

なお，下で展開されている 『速度の２乗に比例する抵抗』 をご覧になったかと思いますが，その中で やかんさんが紹介しておられる 質点の力学３ http://www.hepl.phys.nagoya-u.ac.jp/~iijima.nagoya/lect/ppt05.pdf が参考になると思います．

また，上に Joh さんが書いておられるように，テニスボールのように高速回転する物体の運動の場合，回転の効果が無視できません．参考になりそうなサイトをいくつか紹介します．やや難しいものもありますが…

テニスボールのパラドクス

• http://members.jcom.home.ne.jp/1228156001/s-tennisball.html

ＰＣクラスターが変える流体力学

• http://www.pccluster.org/symp/1st/symposium/himeno.pdf#search= '%E6%B5%81%E4%BD%93%E5%8A%9B%E5%AD%A6%E3%80%80%E7%90%83%E3%81%AE%E5%9B%9E%E8%BB%A2'

野球の変化球と流れ

• http://www.nagare.or.jp/nagare/20-6/himeno.pdf#search= '%E6%B5%81%E4%BD%93%E5%8A%9B%E5%AD%A6%E3%80%80%E7%90%83%E3%81%AE%E5%9B%9E%E8%BB%A2'

kira さんのレス (2006/06/11(Sun) 14:31)

山旅人さん，返信ありがとうございました．紹介してくれたサイトをこれから見て，勉強してみようと思います(多分また，わからない記号や計算が出てくるだろうとは思いますが・・・)．

kira さんのレス (2006/06/14(Wed) 00:00)

以前は回答ありがとうございました．その後，少し調べてみたところ，

• http://www.asahi-net.or.jp/~qq8a-tdn/physics/throw2.html

というサイトに

Ｔ= 1/k In (Vo+g/k)/(g/k)

という式があったのですが，”Ｉｎ”というのは何ですか？なにかの記号なんですか？

Joh さんのレス (2006/06/14(Wed) 00:38)

Inじゃなくて，ln(エルとエヌ)で，自然対数を底とする対数の意味です．

kira さんのレス (2006/06/22(Thu) 23:37)

ｌｎ（エルとエヌ）の意味が解りました．ありがとうございます．基本的なことも解らずにすいません．

ところで，山旅人さんの返信で 質点の力学３

• http://www.hepl.phys.nagoya-u.ac.jp/~iijima.nagoya/lect/ppt05.pdf

というサイトを参考に勉強していたのですが， 「粘性抵抗を受ける落体の運動」のページに「β」の記号が出てくるのですが， このページに表記されているすべての「β」は，「物理のがぎしっぽ」で扱われている，空気抵抗「ｋ」と同じものなのでしょうか？ それとも「β」は

なのでしょうか？

また，「抵抗力」のページには， 粘性抵抗(速度が小さいとき)，慣性抵抗(速度が大きくなると効く）と書いてありますが，テニスボールの場合，粘性抵抗・慣性抵抗はそれぞれ時速何キロくらいのときに働いてくるのでしょうか？ ちなみにテニスボールは直径およそ6.5ｃｍ重さおよそ5.6ｇくらいです． また，去年スピードコンテストというイベントがありまして，初速かどうかもわかりませんが，私のサーブの速度は時速170ｋｍということらしいです．世界最速は250ｋｍくらいだったと思います．

山旅人 さんのレス (2006/06/24(Sat) 10:49)

> 「β」は，「物理のがぎしっぽ」で扱われている，空気抵抗「ｋ」と同じものなのでしょうか？

役割はほとんど同じものですが，イコールではありません．すなわち，ｋ＝ｍβ です．どちらを用いるかは好みの問題ですが，私は，β を用いた方が，その後の式がいくらかシンプルになり見やすくなるかと思います．

> テニスボールの場合，粘性抵抗・慣性抵抗はそれぞれ時速何キロくらいのときに働いてくるのでしょうか？

『質点の力学３』 のデータを基に計算してみました．

・粘性抵抗 R ₁ ＝6πaηv＝6×3.14×(6.5×10 ^-2 [m])×(1.8×10 ^-5 [kg/m・s])×v[m/s]≒<b>2.2×10 ^-5 v [N]</b> ・慣性抵抗 R ₂ ＝(π/4)ρ ₀ a ² v ² ＝3.14/4×1.2[kg/m ³ ]×(6.5×10 ^-2 [m]) ² ×(v[m/s]) ² ≒<b>4.0×10 ^-3 v ² [N]</b>

テニスボールのような大きな物体の場合には，始めから <b>慣性抵抗の方が大きい</b> ようですね．

kira さんのレス (2006/06/26(Mon) 21:15)

たびたび返信ありがとうございます．計算は良く解りませんが慣性抵抗のほうが大きいようですね．慣性抵抗と粘性抵抗では落体の運動の式が変わってくるのでしょうか？紹介された「質点の力学」の「慣性抵抗」のページの計算式は，ますますわからないので，とりあえず「粘性抵抗を受ける落体の運動」のページでまた質問があるのでよろしくお願いします． （・・・うまく表示されてるでしょうか？) 初期条件として

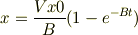
という式がありましたが，その式からtを求めると

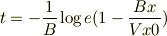
で良いのでしょうか？また，もっと簡単な式にはならないのでしょうか？ そしてyの初期条件として

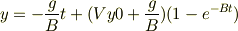
となっていますが，頑張って計算しても

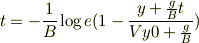
となってしまい，logの中にもｔが入ってたりして，結局計算できないのですが，この後はどういう風にすればいいのでしょう？

山旅人 さんのレス (2006/06/27(Tue) 23:36)

> 慣性抵抗と粘性抵抗では落体の運動の式が変わってくるのでしょうか？

「ある速さまでは，粘性抵抗がはたらき，それより速くなると慣性抵抗がはたらく」 と誤解されていませんか？ <b>どのような速さのときにも，粘性抵抗も慣性抵抗もつねにはたらく</b> のです． 空気の抵抗は，速さ v に関係するので，R(v) と書かれます．これを v について展開すると

R(v)＝a ₁ v＋a ₂ v ² ＋a ₃ v ³ ＋…

この第１項を粘性抵抗，第２項を慣性抵抗とよぶのです．第３項以降も考えられるわけですが，ここまで考慮しても運動方程式が解析的に解けなくなるので，私はここまで書いてある本を見たことがありません．

> x＝V _x0 </sub>/β)(1−e ^-βt )→t＝(−1/β)log(1−βx/V _x0 </sub>) あっています．これ以上簡単な式にはなりません．

その下の y の式には，t が１次の項と e の肩の両方に含まれているので，これを t＝… の形に解くことはできません．ですから，この式で y を与えて t を求めさせられることは，おそらくないと思います． どうしてもというのならば，エクセル等で数値計算をして，逐次近似で精度を上げていくしか方法はありません．

kira さんのレス (2006/06/30(Fri) 00:18)

たびたび返信ありがとうございます．山旅人さんの言うとおり慣性抵抗と粘性抵抗のことは勘違いしていたようです． ところでｘの式なんですけれども，もし初期条件で風が吹いているような場合，その風による加速度を含めた式に直すと，ｙの式のｇの部分を置き換えればよいのでしょうか？その場合，やはりその式にｘを与えてｔを求めさせることはできないのでしょうね．

なんとかｘ，ｙを与えてｔを求める方法を知りたかったのですが，残念です．ですが，何ヶ月たったか解りませんが，仕事の合間にいろいろ調べたり考えたりして，答えがあるのかないのかすら分からないまま，ちょっと疲れてきたところだったので，はっきり計算できないといわれて，逆に少しホッとした感じがします．今まで返信くださった方々様，本当にありがとうございました．

山旅人 さんのレス (2006/07/01(Sat) 10:28)

> もし初期条件で風が吹いているような場合，… ，ｙの式のｇの部分を置き換えればよいのでしょうか？

『風』 は文字どおり空気の抵抗ですから，「ｇの部分を置き換え」 ではないですね．状況 （風の方向とか速さとか） をもっと正確に書いていただければ，も少しきちんとした回答ができるかと思います．

> はっきり計算できないといわれて，

上記したように，「できない」 のではありません．電卓のボタンを押すと答がパッというわけにはいかないというだけです．省力化したければプログラム（エクセルのマクロ等）を組むことになるわけで，そのためのアルゴリズム（計算手順）もいくつも開発されています．