速度の2乗に比例する抵抗
速度の2乗に比例する抵抗
リキ さんの書込 (2006/06/05(Mon) 23:42)
大学1年の理工学部で学んでいる者です.現在力学で運動方程式の積分などを中心に学んでいます.以下の問題が分かりません.
「質量mの質点が速さvで運動しているとき,速度の2乗に比例した空気の抵抗kv^2を受けるとする.初速度v0で鉛直下方に投げた後の速度の変化を調べる.重力加速度をgとしたときv(t)を求めなさい.」
自分で途中まで解いたのですが,めちゃくちゃになってしまいよく分かりません. とりあえず運動方程式が
m*dv/dt=mg−kv^2
になって変数分離をして,それを部分分数分解するところまでは分かるのですが,二重根号が出てきてしまったり計算に行き詰ってしまいました.答えとその導出方法が分かる方は教えていただけると嬉しいです.お願いします.
Re: 速度の2乗に比例する抵抗
トンガリ さんのレス (2006/06/06(Tue) 15:09)
導出方法は書いてありませんが,答えだけなら,下記にあります. Saturnの第4章雨滴の落下速度(水滴が大きいとき)
Re: 速度の2乗に比例する抵抗
やかん さんのレス (2006/06/06(Tue) 17:02)
http://www.hepl.phys.nagoya-u.ac.jp/~iijima.nagoya/lect/ppt05.pdf
10ページあたりが参考になるでしょうか.微分方程式は四半世紀も解いてないので すみません・・・.
Re: 速度の2乗に比例する抵抗
トンガリ さんのレス (2006/06/06(Tue) 17:40)
『 部分分数分解(だっけ?)すると 変数分離形になる 』もある. 物理難民を救うページの 重力による質点の運動(抵抗が速度の2乗)
Re: 速度の2乗に比例する抵抗
toorisugari no Hiro さんのレス (2006/06/06(Tue) 19:03)
上に紹介されたURLはみていませんが,下向きの速度を持つときは 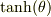 で置き換えるのが常道ではないですか?
で置き換えるのが常道ではないですか?
上向きの時はちょっと前に同じ問題がでていますね.このときは 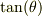 で置き換えてますね.
で置き換えてますね.
Re: 速度の2乗に比例する抵抗
山旅人 さんのレス (2006/06/06(Tue) 21:13)
トンガリさんご紹介のサイトは,2つとも 「雨滴の落下速度」 となっており,暗黙裏に初期条件 t=0 のとき v=0 が仮定されているようです.ですので,本スレッドの要請を,肉薄はしているものの満たしていません.
正しくは,第2のサイト http://www14.plala.or.jp/phys/mechanics/10.html の下から6行目を (m/2Ak)log[(A+v)/(A-v)]=t<b>+C'</b> とし,これから,
(A+v)/(A-v)=Cexp(2Ak/m)t
初期条件t=0 のとき v=v 0 より,C=(A+v 0 )/(A-v 0 ) で,最終結果は,
<b>v=√(mg/k)[v 0 +√(mg/k)tanh√(kg/m)t]/[√(mg/k)−v 0 tanh√(kg/m)t]</b>
となります.teX が使えないので,見にくくてすいません.
Re: 速度の2乗に比例する抵抗
山旅人 さんのレス (2006/06/06(Tue) 23:05)
上に自分で書いた式のキタナさに辟易としながら,次のように書いた方がわかりやすいか,と考えました.
<b>v=√(mg/k)tanh{√(kg/m)(t+t 0 )}</b>
ただし,v 0 =√(mg/k)tanh{√(kg/m)t 0 },t 0 =√(m/gk)tanh -1 {√(k/mg)v 0 }
Re: 速度の2乗に比例する抵抗
toorisugari no Hiro さんのレス (2006/06/06(Tue) 23:12)
すでに改良版がでてますが
> v=√(mg/k)[v0+√(mg/k)tanh√(kg/m)t]/[√(mg/k)−v0tanh√(kg/m)t]
分母の-は+のtypoですよね.
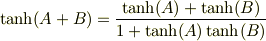
ですから.
Re: 速度の2乗に比例する抵抗
リキ さんのレス (2006/06/06(Tue) 23:43)
とても馬鹿な質問をしているかもしれませんがお願いします.物理難民を救うページで部分分数分解をしていますが,そのとき分子を1にそろえるために1/2Aを掛けています.ですが,1/(A+v)-1/(A-v)の計算結果は
-2v{1/(A^2-v^2)}になるのではないんですか?
Re: 速度の2乗に比例する抵抗
toorisugari no Hiro さんのレス (2006/06/06(Tue) 23:53)
> 1/(A+v)-1/(A-v)の計算結果は-2v{1/(A^2-v^2)}になるのではないんですか?
該当するページの記述が間違っています.
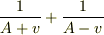 のtypoですね.
のtypoですね.
Re: 速度の2乗に比例する抵抗
リキ さんのレス (2006/06/07(Wed) 00:39)
みなさんにお礼を言うのを忘れていました.みなさん親切にたくさんの返事を有難うございます.
>toorisugari no Hiroさん typoとはなんですか?
Re: 速度の2乗に比例する抵抗
リキ さんのレス (2006/06/07(Wed) 00:44)
了解です.もう一度自分でも解きなおしてみます. tanhX=(e^X-e^X)/(e^X+e^X)という認識で合っていますでしょうか?
Re: 速度の2乗に比例する抵抗
toorisugari no Hiro さんのレス (2006/06/07(Wed) 00:48)
> tanhX=(e^X-e^X)/(e^X+e^X)という認識で合っていますでしょうか? 0になってしまいますよ.
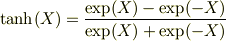
Re: 速度の2乗に比例する抵抗
リキ さんのレス (2006/06/07(Wed) 00:49)
あ,そうです.これでした.typoです. 解いてみます.みなさん有難うございました.解いてみて分からなければまたお願いいたします.
Re: 速度の2乗に比例する抵抗
リキ さんのレス (2006/06/07(Wed) 19:16)
どうしても計算できません!またまた申し訳ありませんがお願いします. とりあえず部分分数分解の部分が足し算に変わったので,logの部分も積の形になると思われるのですが・・. というか前のlog/logの形になっているものもどうやって解けばいいのか分かりません.
Re: 速度の2乗に比例する抵抗
リキ さんのレス (2006/06/07(Wed) 20:08)
あ,そうですよね..それで−になるので分数log/logの形になるわけですね. それで v=√(mg/k)×{1-Cexp(2Akt/m)}/{1+Cexp(2Akt/m)}
になりますよね?ここでどのようにtanhtを適用するんですか?
Re: 速度の2乗に比例する抵抗
山旅人 さんのレス (2006/06/07(Wed) 22:13)
だいぶ上の方に行ってしまいましたが,
> 分母の−は+のtypoですよね.
toorisugari no Hiro さん,ご指摘有難うございました.typo ではなく確信犯の計算ミスでしたが…
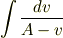
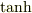 の定義としばらく「にらめっこ」してください.
の定義としばらく「にらめっこ」してください.