大学物理

AI さんの書込 (2006/05/28(Sun) 21:02)

大学の中間テストの問題なのですが．流速V，河幅ｌの河のO点の対岸Pから船速Vの船が常に船首をO点に向けて進むとき，船は岸のどこに到着するだろうか．O点からの距離を求めよ．というものですが，船首を常にO点に向けるということはθがつねに変化しますよね．考えているのですが，このような問題はどんな方針で解けばいいのかよくわかりません．わかる方がいればどうか教えてください．

Re: 大学物理

yama さんのレス (2006/05/29(Mon) 00:17)

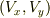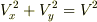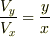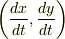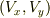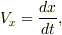
O点を原点とし川岸をy軸にとった座標系を考えます．対岸をx＝-l とし，水はy軸の負の向きに速さ V で流れているとします．水に対する船の速度を (V_x,V_y) とすると V_x^2+V_y^2=V^2 が成り立ちます．また，常に船首をO点に向けるということは，この速度の向きがOの向きになるということなので次の式が成り立ちます． $\frac{V_y}{V_x}=\frac{y}{x}$ 一方，川岸に対する船の速度 $\left(\frac{dx}{dt},\frac{dy}{dt}\right)$ と水に対する船の速度 (V_x,V_y) の間には次の関係があります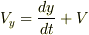． $V_x=\frac{dx}{dt},$ $V_y=\frac{dy}{dt}+V$ 初期条件を「t＝0 のときx＝-l，y＝0」としてこれらの方程式を解き，x＝0 の時の y の値を求めればいいでしょう．しかし，これらの方程式は簡単に解けそうには見えませんが・・・．

Re: 大学物理

Joh さんのレス (2006/05/29(Mon) 01:29)

少し進んだ場所で極座標で考えてみると，船がP点に向かうスピードは 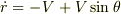$\dot{r}=-V+V\sin \theta$ ，直交する方向へのスピードは 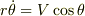$r\dot{\theta}=V\cos \theta$ と書けそうですから，これを 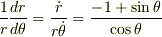$\frac{1}{r}\frac{dr}{d\theta}=\frac{\dot{r}}{r\dot{\theta}}=\frac{-1+\sin \theta }{\cos \theta }$ と組み合わせたらどうでしょう？変数分離形ですから，そのまま積分できると思います．（logがたくさん出てきそうですね・・・）軌跡の方程式を求めるのが問題ですか？

Re: 大学物理

yama さんのレス (2006/05/29(Mon) 09:15)

なるほど，極座標で考えれば何とかなりそうですね．ところで，流れに垂直な速度成分は，岸に近づくとほぼ指数関数的に限りなく小さくなっていくので，有限時間では岸に到着できないように思います．もちろん，岸のある点に限りなく近づくので，その極限点までの距離を求めればいいのだと思いますが，有限の時間では到着できないとすると「船は岸のどこに到着するだろうか．」という表現はいかがなものか・・・．

Re: 大学物理

トンガリさんのレス (2006/05/29(Mon) 13:45)

AIさんの『どんな方針で解けばいいのか』，が印象的であった．

１．渡る時間を最小にする航法は，流れに垂直に進む航法で，最小渡り時間I/Vを得る．２．最小渡り時間I/Vで流される距離はIである．３．船首を常にO点に向ける航法では，流されまいと終始努力しているので，努力を評価して私なら直感的に，中を取って流される距離を半分に見積もる．４．この船は時間が掛かるが，流される距離I/2の岸に限りなく近付くであろう．

Re: 大学物理

toorisugari no Hiro さんのレス (2006/05/29(Mon) 17:34)

$\frac{dr}{r}=\frac{-1+\sin \theta }{\cos \theta }d\theta$

の式の右辺の分子分母に 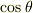$\cos \theta$ をかけて変形して計算すると，

> ４．この船は時間が掛かるが，流される距離I/2の岸に限りなく近付くであろう．

トンガリさんの予想が正しそうですね．積分計算以外にもっと簡単な方法はないのでしょうかね．

Re: 大学物理

AI さんのレス (2006/05/29(Mon) 21:13)

返信ありがとうございます．助かりました．

川を渡る船

山旅人さんのレス (2006/05/29(Mon) 22:21)

ｙａｍａさんが９６３０でお書きの設定をそのまま使わせていただきます．

Ｖ _x ² ＋Ｖ _y ² ＝Ｖ ² … (1) Ｖ _y /Ｖ _x ＝ｙ/ｘ … (2) より，Ｖ _x ＝（−ｘ/√（ｘ ² ＋ｙ ² ））Ｖ，Ｖ _y ＝（−ｙ/√（ｘ ² ＋ｙ ² ））Ｖ … (3)

また，ｄｘ/ｄｔ＝Ｖ _x ，ｄｙ/ｄｔ＝Ｖ _y −Ｖ … (4)

(3)(4)より，ｄｙ/ｄｘ＝（Ｖ _y −Ｖ）/Ｖ _x ＝ｙ/ｘ＋√（１＋（ｙ/ｘ） ² ） … (5)

(5)は同次形の微分方程式で，そう難しくなく解ける．初期条件（ｘ＝−Ｌでｙ＝０）を満たす解は， <b>ｙ＝ｘ ² /（２Ｌ）−Ｌ/２</b> … (6)

(6)が船の航跡の方程式で，船は，Ｏから <b>Ｌ/２</b> 離れた点にたどり着く．

Re: 川を渡る船

yama さんのレス (2006/05/29(Mon) 23:37)

なるほど，同次型になるのですね．これだと，航跡が放物線になることが一目瞭然ですね．

Re: 川を渡る船

トンガリさんのレス (2006/05/31(Wed) 18:08)

流れに垂直に進む航法とこの航法を比較する．

１．この航法では，流される距離は半分になる．(解決済み) ２．この航法では，航跡の長さに変わりがない．(解決済み) ３．この航法では，岸に限りなく近付く時間は直感的にπ倍となるであろう．

Re: 川を渡る船

toorisugari no Hiro さんのレス (2006/06/01(Thu) 21:30)

問題は解決してるのですが，到着時間が気になったので計算してみました．(積分計算は挫折してMapleさんに頼りましたが．．．)

$\theta$ になるまでの時間は

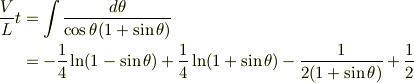
$\frac{V}{L}t &= \int\frac{d\theta}{\cos\theta(1+\sin\theta)}\\&=- \frac{1}{4}\ln(1-\sin\theta)+ \frac{1}{4}\ln(1+\sin\theta)- \frac{1}{2(1+\sin\theta)}+ \frac{1}{2}$

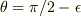なので $\theta=\pi/2-\epsilon$ になるまでの時間は

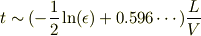
$t \sim (-\frac{1}{2}\ln(\epsilon)+0.596\cdots)\frac{L}{V}$

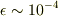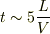となり(前半だけなら手計算でもでますね)，到達まで予想通り無限の時間がかかりますが，たかがlog orderです． $\epsilon \sim 10^{-4}$ なら $t \sim 5\frac{L}{V}$ くらいで到着ですね．（ちなみに川の真ん中までは 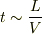$t \sim \frac{L}{V}$ くらいです．)

Re: 川を渡る船

山旅人さんのレス (2006/06/03(Sat) 23:12)

直交座標による考察も載せておきましょう．

前記（No.9646）の(3)(4)(6)より，

√（ｘ ² ＋ｙ ² ）＝√（ｘ ² ＋（ｘ ² /２Ｌ−Ｌ/２） ² ）＝ｘ ² /２Ｌ＋Ｌ/２ ∴ ｄｔ/ｄｘ＝−√（ｘ ² ＋ｙ ² ）/Ｖｘ＝−（１/Ｖ）（ｘ/２Ｌ＋Ｌ/２ｘ）

よって，川を渡りきるのに要する時間Ｔは，

Ｔ＝−(１/Ｖ）∫ _-L ⁰ ）（ｘ/２Ｌ＋Ｌ/２ｘ）ｄｘ

この積分は無限大に発散するので，ε＝−１０ ^-n Ｌまで岸に近づくには，

Ｔ _n ＝−（１/Ｖ）[ｘ ² /４Ｌ＋（Ｌ/２）ｌｏｇ|ｘ|] _-L ^ε ＝−ε ² /４ＬＶ−（Ｌ/２Ｖ）ｌｏｇε＋（Ｌ/２Ｖ）（１/２＋ｌｏｇＬ）〜（Ｌ/Ｖ）（１/４＋ｎ・ｌｏｇ１０/２）〜（Ｌ/Ｖ）（０．２５＋１．１５ｎ）

[home] [掲示板] [ページの先頭]