oshiro さんの書込 (2006/05/25(Thu) 23:19)

小球が半円型の斜面を転がるときの速度変化を，（微分方程式？で)あらわしたいのですが． 本来なら，絵が描ければ場面を思い浮かべられると思うのですが・・・ ローラースケートの競技場みたいな，半円のところを，小球が転がるときの速度変化です，摩擦は完全に無視できるとします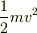． みたいな式があったと思いますが，速度変化までは表せないような気がするので，誰かご助言願います．

yama さんのレス (2006/05/26(Fri) 00:18)

エネルギーの保存を利用するといいでしょう． 運動エネルギーは，並進運動のエネルギー 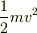と回転のエネルギー 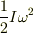との和になります．これとポテンシャルエネルギーとの和が保存されます． 慣性モーメント I は球の半径 r と質量 m で表し，角速度 ω は r や v などで表します． 平面上を転がる場合は，v＝rω ですが，半円形の斜面上では少し違うことに注意しましょう．

トンガリ さんのレス (2006/05/26(Fri) 12:30)

oshiroさんの直感どおり， エネルギーの保存の式からは，速度変化までは表せない．

エネルギーの保存の式は，[始点]のエネルギー＝[終点]のエネルギー，で表される． [始点]〜[終点]の移動経路には無関係で，したがって時間経過にも無関係である．

移動経路に無関係なのを利用して，円弧の谷や山を落下する物体の[終点]速度を容易に式化できる． 時間経過に無関係なことの欠点は，エネルギーの式を運動方程式(微分方程式)に利用できない．

また?繰返し?の様ですが， 重力による円弧運動の運動方程式(微分方程式)は私の数学力では近似式でしか解けない． したがって解の式は，振り子の近似式と同様に，円弧の谷付近でしか成り立たない． 式が成り立つには，[始点]〜[終点]が円弧の谷付近でなければならず， このテーマでは，もっと高い所に[始点]があると，私は推察する．

運動方程式(微分方程式)の演習には，あまり難解なものは適さない． パソコンや表計算が発達した現在では，解析的に解く努力をするより，数値計算するのが実用的だ． 例えば円弧を90分割した各速度や経過時間を知りたいなら， エネルギーの保存の式，[始点]のエネルギー＝[終点]のエネルギー，を90回使えば良いではないか． 経過時間も各距離÷各速度を数値積分して数値計算できる．

テーマの，小球が半円型の斜面を転がるときの[終点]のエネルギーは運動エネルギ−であるが， 大円穴の内面を転がる小円筒の角速度と，小円筒の重心移動速度の幾何学的件(遊星歯車)を利用して， 運動エネルギーを，並進運動と回転の2つのエネルギーに，一定比率に分配可能である．

したがって，パソコンや表計算を使って，容易に数値計算できる． 運動方程式(微分方程式)の演習には，このテーマは難解で止めたが良い．

ｙama さんのレス (2006/05/26(Fri) 14:32)

>時間経過に無関係なことの欠点は，エネルギーの式を運動方程式(微分方程式)に利用できない．

これは違います．エネルギーの式は運動方程式から導かれるもので，自由度が１の場合はこれを利用して，速度を座標の関数として表すことができます． 速度は座標を時間で微分したものなので，これによって１階の微分方程式が得られたことになります． これを解けば座標が時間の関数として求められ，それを時間で微分すれば，速度が時間の関数として求められます． この問題の場合は単振子の場合と同様な式になるため，解は楕円関数で表されることになりそうです． 数値で求める場合は，トンガリさんが言われるようにパソコンで数値積分したほうがいいかもしれません．

トンガリ さんのレス (2006/05/26(Fri) 17:31)

エネルギーの保存の式は，[始点]のエネルギー＝[終点]のエネルギー エネルギーの式は，位置エネルギーmgh，運動エネルギー0.5mv^2，仕事∫Fds

運動方程式(微分方程式)は加速度(あるいは力)の関係式なので， 運動方程式の中にエネルギーの式を直接書き込むことは不可能． 私はエネルギーの式を加速度(あるいは力)の式に変える方法を知らない． エネルギー保存の式mgh=0.5mv^2は，微分方程式h''＝g(あるいはmh''＝mg)を解いて，tを消去して得た．

それはさておき， 争点をまとめると， yamaさん『エネルギーの式は運動方程式から導かれるもので，』 トンガリ『エネルギー保存の式は運動方程式から導かれるもので，』

ｙama さんのレス (2006/05/26(Fri) 18:08)

『エネルギーの式』というのを『エネルギー保存の式』という意味に受け取っていたのですが，これは間違いでしたね．トンガリさんの言われる通り，『エネルギー保存の式は運動方程式から導かれるもので，』というのが正しいです． それはともかく，エネルギー保存の式を利用して速度変化を求めることができることは，説明した通りです．ただし，説明の中の『エネルギーの式』は『エネルギー保存の式』に置き換えてください． なお，私の言う『エネルギー保存の式』は，単に始点と終点のエネルギーが等しいというのではなく，全時刻でエネルギーが一定に保たれることを表す式で，『エネルギーの積分』とも言われる式のことです．

トンガリ さんのレス (2006/05/27(Sat) 11:24)

yamaさんの言う『エネルギーの積分』の式の概念を私は知らない．それでも私は， エネルギー＝微小エネルギーの総和＝例えば仕事∫Fds，の概念なら理解できる． 適用例として，位置エネルギー＝∫Fds＝∫mgdh＝mghを得る．

このテーマの主題であるoshiroさんの質問の主旨は， 例えば運動エネルギーの式0.5mv^2を運動方程式(微分方程式)に利用できるや否や． に相違ない．

争点をまとめると， トンガリ『oshiroさんの直感どおり， エネルギーの保存の式からは，速度変化までは表せない．』 トンガリ『運動エネルギーの式0.5mv^2を運動方程式(微分方程式)に利用できない．』 yamaさん『これは違ます．・・・・・』 yamaさん『エネルギー保存の式を利用して速度変化を求めることができることは，説明した通りです．』

私の主張に変わりはないが，説得に窮して，今は説明する言葉の持ち合わせがない． そこで，仮に『エネルギー保存の式を利用して速度変化を求めることができる』のなら， yamaさんに，何でも宜しいですので，運動方程式の具体例を示して教えて頂きたい．

oshiro さんのレス (2006/05/27(Sat) 12:43)

ありがとうございます． どうやら，皆様方知識人をもってしてでも難しい問題のようですので， 私が理解するにはちょっと壁が高すぎるかもしれません． 速度変化の公式があるものだと思っていましたが， 今回は，やはり地道に計算していったほうがよいのでしょうか？

yama さんのレス (2006/05/27(Sat) 23:36)

速度変化を求めることはできますが，計算は面倒で，結果も初等関数では表せません．具体的な数値を求めたいなら，数値積分を用いたほうがいいでしょう．

次に，トンガリさんの質問に答えておきます． 例として鉛直投射を考えます．この場合は，運動方程式 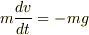をそのまま積分して 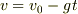を得ることことができるので，エネルギーの保存を利用する必要はないのですが，次のようにエネルギーの保存を利用して速度変化を求めることもできます． まずエネルギーの保存は次の式で表されます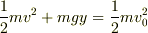． これを v について解くと 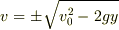となります． ± のどちらをとるかで，場合分けが必要ですが，ここでは＋の場合を考えます． v＝dy/dt ですから，次の微分方程式が得られます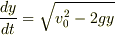． これは変数分離型なので次のように積分できます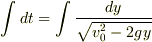． 積分を計算すると次の式が得られます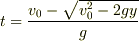． ここで積分定数の値は初期条件（t=0 のときy=0）を満たすように定めています． これを y について解くと 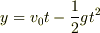となります． 従って，速度は 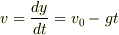と求められます．

トンガリ さんのレス (2006/05/28(Sun) 10:33)

エネルギーの式は，位置エネルギーmgh，運動エネルギー0.5mv^2，仕事∫Fds 私はエネルギーの式を加速度(あるいは力)の式に変える方法を知らない．

私は先に上記の様に述べた．0.5mv^2の他に付いては誤りの様だ． ここで，位置エネルギーと新知識『保持力』を使う．

重力の位置エネルギーE(h)＝mgh を高さhで微分してマイナスを付けると，『保持力』＝-mg，を得る． 重力mgを受ける物体を，現在位置に『保持』するには『保持力』が必要，と納得する．

バネ定数kの場合の位置エネルギーE(s)＝∫Fds＝∫ksds＝0.5ks^2 をタワミsで微分してマイナスを付けると，『保持力』＝-ks，を得る． バネ力ksを受ける物体を，現在位置に『保持』するには『保持力』が必要，と納得する．

しかし，得られる結果は常識の範囲内であって，『保持力』に特段の効能を感じない． hやsは『位置』を表す変数だったので『保持力』を得られたが，ｖではそうは行かない．

＜追伸＞ エネルギー保存の式から，v^2＝v．^2−2gh，したがって，0.5mv^2＝0.5m(v．^2−2gh) までは常に成り立つ． 最後の式E(h)を高さ-hで微分してマイナスを付けると，『保持力』＝-mg，を得る． ただし，この微分はｖがｈと同一方向を保つ時，すなわち鉛直投射or落下の場合に限る． したがって，円弧面上の落下を含む一般の場合のｖではそうは行かない．

【広く質問】 新知識『ポテンシャル』や『保持力』の概念を全く理解してない者ですが， １．『ポテンシャル』を微分するとは，『ポテンシャル』が増加する方向の符号で微分する意味か． ２．論理物理学で『ポテンシャル』や『保持力』の概念を使う効能を教えて下さい．

トンガリ さんのレス (2006/05/28(Sun) 13:29)

【自習】 回転座標系の位置エネルギーE(ｒ)＝∫Fds＝∫−mω^2ｒdｒ＝E．−0.5mω^2ｒ^2 を半径−ｒで微分してマイナスを付けると，『保持力』＝−mω^2ｒ，を得る． 遠心力mω^2ｒを感じる物体を，現在位置に『保持』するには『保持力』が必要，と納得する．

得られる結果は常識の範囲内であって，やはり『保持力』に特段の効能を感じない． それでも，自分が立てた式の点検に役立つのは確かだ．

yama さんのレス (2006/05/28(Sun) 21:03)

ポテンシャルエネルギーを座標で微分してマイナスを付けたものは，『保持力』ではなくて『保存力』です．保存力による運動では全エネルギーが保存します．

ポテンシャルエネルギーを x で偏微分してマイナスを付けたものは，保存力のx成分です．すなわちポテンシャルエネルギーを U(x,y,z) とすると 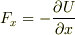となります．y成分,z成分についても同様です． このため，保存力の向きは，ポテンシャルエネルギーの減少する向きになります．

ポテンシャルや保存力の概念は，エネルギーの保存を定式化するのに役立ちます． また，力はベクトル量のため一般には３成分を持ちますが，ポテンシャルはスカラー量のため１つの数値だけで表されます．２つの力を合成するとき，直接ベクトルとして合成するより，それらの力のポテンシャルの和を座標で微分したほうが計算が簡単になることがあります．