ラグランジュの運動方程式

home > 掲示板 >

このページのPDF版

サイトマップ

ラグランジュの運動方程式

高陽さんの書込 (2006/05/23(Tue) 17:27)

はじめまして，大学一年の高陽という者です．ラグランジュの運動方程式についての質問です．

L[x,y]=T[x',y']-U[x,y] （「'」は時間微分）において， ∂L/∂x'=∂T/∂x' となりますが，これは ∂U/∂x'=0 から導かれるようです．ここで， ∂U/∂x'=（∂U/∂x）（∂x/∂x'）と変形すれば，（∂U/∂x）≠0のとき，（∂x/∂x'）=0（xはx'に依存しない）とならなければなりません．しかし，（∂x/∂x'）=（∂x/∂t）（∂t/∂x'）=x'/x'' と変形すれば，常に（∂x/∂x'）=0が成立するとは思えないのですが．なぜ（∂x/∂x'）=0，となるのでしょうか？いろいろと調べたのですが，いずれもこの点にはほとんど触れられていませんでした．

Re: ラグランジュの運動方程式

toorisugari no Hiro さんのレス (2006/05/23(Tue) 18:10)

物体の軌道を 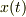x(t) と考えると速度は 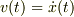$v(t)=\dot x(t)$ の関係があり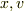， x,v のふたつが独立とは思えないと言うご質問でよろしいですね．

軌道を最初から考えるから混乱します．

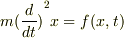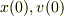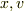$m{(\frac{d}{dt})}^2 x = f(x,t)$ の方程式を満たす軌道は任意の初期条件 x(0),v(0) で存在します．つまり， t=0 では x,v を独立に選べるわけです．(選択される軌道が変わりますが．．．)

軌道を忘れてしまえば，各時刻の「初期」条件のペア 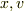x,v を別々に考えることができ，かつ，それぞれを独立にできます．

その組の中で条件を満たすものを探すと言う問題です．

Re: ラグランジュの運動方程式

高陽さんのレス (2006/05/23(Tue) 19:36)

一般解の任意定数は，x,v，の（独立な）初期条件に応じて与えられる．従って，x,v，は独立，ということでよろしいですか？

では，物理としてではなく，数学として dx/dx'という式だけを見たときにはどう解釈すればよいでしょうか？

Re: ラグランジュの運動方程式

toorisugari no Hiro さんのレス (2006/05/23(Tue) 21:42)

> dx/dx'という式だけを見たときにはどう解釈すればよいでしょうか？

常微分ですか?どういうところで現れるか教えてくれませんか?

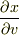$\frac{\partial x}{\partial v}$ のことなら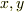， x,y 座標における 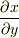$\frac{\partial x}{\partial y}$ と同じ扱いですが．

Re: ラグランジュの運動方程式

yama さんのレス (2006/05/23(Tue) 23:19)

ラグランジアンを座標だけの関数 L[x,y] と考えるのは正しくありません．座標と速度の関数 L[x,y,x',y'] と考えるべきものです．もちろん，座標と速度の間には x'＝dx/dt のような関係があるので，速度は座標の関数であるともいえます．しかし，これらを形式的に独立な変数とみなしてラグランジュ方程式を計算することによって正しい運動方程式が得られるというわけです．

Re: ラグランジュの運動方程式

高陽さんのレス (2006/05/24(Wed) 20:45)

>>yamaさんでは，（ラグランジュとは関係なく）逆に独立な変数とみなせない場合というのはどういう場合ですか？具体的に時刻の関数として，位置，速度が与えられた場合ですか？

Re: ラグランジュの運動方程式

yama さんのレス (2006/05/24(Wed) 22:31)

速度を x' のように表したのはちょっとまずかったかもしれませんね．これだと x の時間微分ということになってしまうからです． 'は時間微分ではなく，x と異なる変数であることを示すための記号と考えるべきです．つまり，ラグランジアンにおいては，x'＝dx/dt という関係は無視して x と x' を（形式的に）互いに独立な変数とみなすわけです．しかし，そのラグランジアンから導かれた運動方程式では，x' は x の時間微分であると考えます．

Re: ラグランジュの運動方程式

高陽さんのレス (2006/05/24(Wed) 23:12)

「ラグランジアンにおいては，x'＝dx/dt という関係は無視して x と x' を（形式的に）互いに独立な変数とみなす」（うまく伝わらなかったのかもしれないので，繰り返しになりますが）逆に，xとx'が独立と考えてはいけない場合というのはどういう場合ですか？（あるいは，ラグランジアン以外に独立とみなせる場合は？）

Re: ラグランジュの運動方程式

toorisugari no Hiro さんのレス (2006/05/24(Wed) 23:16)

> 逆に，xとx'が独立と考えてはいけない場合というのはどういう場合ですか？

繰り返しですが，Euler-Lagrange方程式が得られた後です．

Re: ラグランジュの運動方程式

toorisugari no Hiro さんのレス (2006/05/25(Thu) 01:35)

> 繰り返しですが，Euler-Lagrange方程式が得られた後です．

言葉が正確でなかったので書き直します．

Euler-Lagrange方程式が得られ，Lagrangian 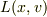L(x,v) の具体的な関数形に対して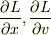， $\frac{\partial L}{\partial x}, \frac{\partial L}{\partial v}$ を計算した後は 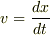$v = \frac{d x}{d t}$ と考えます．このときは 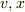v, x は独立ではなくなります．

Re: ラグランジュの運動方程式

高陽さんのレス (2006/05/26(Fri) 22:15)

わかったような気はしますが… またいつか考え直してみます．ありがとうございました．

Re: ラグランジュの運動方程式

toorisugari no Hiro さんのレス (2006/05/26(Fri) 23:36)

どうも質問の意図を読み違えてた気がしてきました．

高陽さんの質問は「Lagrangian 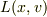L(x,v) のEuler-Lagrange方程式

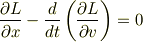
$\frac{\partial L}{\partial x}-\frac{d}{dt}\left(\frac{\partial L}{\partial v}\right)=0$

に対して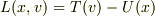， L(x,v)=T(v)-U(x) を与えたとき

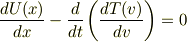
$\frac{d U(x)}{d x}-\frac{d}{dt}\left(\frac{d T(v)}{d v}\right)=0$

がえられる．

この計算時に

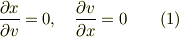
$\frac{\partial x}{\partial v}=0,\quad \frac{\partial v}{\partial x}=0 \qquad(1)$

を使っているが

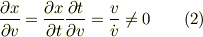
$\frac{\partial x}{\partial v}&= \frac{\partial x}{\partial t}\frac{\partial t}{\partial v}= \frac{v}{\dot v} \ne 0 \qquad(2)$

となり矛盾を感じる．なにが問題なのか?」と言うことでしょうか？

結論を言うと，(2)がまちがってる，すなわち，偏微分を正しく理解されていません．

常微分のchain rule

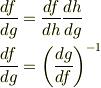
$\frac{df}{dg}&=\frac{df}{dh}\frac{dh}{dg}\\\frac{df}{dg}&=\left(\frac{dg}{df}\right)^{-1}$

をそのまま偏微分に使ってはいけません．偏微分ではなりたちません．

そもそも

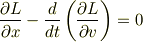
$\frac{\partial L}{\partial x}-\frac{d}{dt}\left(\frac{\partial L}{\partial v}\right)=0$

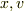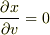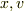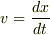の式において x,v はともに独立な変数の組( $\frac{\partial x}{\partial v}=0$ )として考えており，偏微分の計算がすむまでは， x,v がの関数であることや，まして， $v=\frac{d x}{d t}$ といった関係はありません．

Re: ラグランジュの運動方程式

やかんさんのレス (2006/05/27(Sat) 14:36)

は終始独立変数扱いとしても，速度としての定義や，ディメンジョンがあるのに，最後になって $v=\frac{dx}{dt}$ の関係が決まるなんて，不思議な感じもしますね．

Re: ラグランジュの運動方程式

toorisugari no Hiro さんのレス (2006/05/29(Mon) 15:31)

やかんさん > vは終始独立変数扱いとしても，速度としての定義や，ディメンジョンがあるのに，最後になって 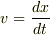$v=\frac{dx}{dt}$ の関係が決まるなんて，不思議な感じもしますね．

確かにそうですね．でも，これは単純に順番の問題です．最初から 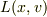L(x,v) でなく具体的な T(v)-U(x) に対して直接変分問題を解くようにすれば，

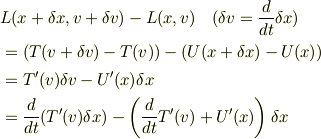
$&L(x+\delta x, v+\delta v)-L(x, v)\quad(\delta v=\frac{d}{dt}\delta x)\\&=(T(v+\delta v)-T(v))-(U(x+\delta x)-U(x))\\&= T'(v)\delta v - U'(x)\delta x\\&= \frac{d}{dt}(T'(v)\delta x) - \left(\frac{d}{dt}T'(v) + U'(x)\right)\delta x$

となり，なにも不思議なことは起きません．

でもこれでは汎用な公式にならない．

結局，変分の操作(偏微分)を(部分積分の)後でやるから不思議なことをしてるように見えるだけだと思います．

Re: ラグランジュの運動方程式

やかんさんのレス (2006/05/29(Mon) 18:28)

toorisugari no Hiroさん，有難うございます．本当は仮想的な変位である 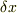$\delta x$ と考えるべきところを，時間微分から本来分けて考えられない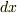と同じように扱うとおかしく感じる，という事でしょうか．

Re: ラグランジュの運動方程式

toorisugari no Hiro さんのレス (2006/05/30(Tue) 04:59)

> 本当は仮想的な変位である 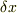$\delta x$ と考えるべきところを，時間微分から本来分けて考えられない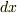と同じように扱うとおかしく感じる，という事でしょうか．

うーん．．．時間微分と結びついてるのは変位の方だと思います．(でないと部分積分ができません)

EL方程式で偏微分がややこしいのは，それが変分計算の名残だから，と思っているのですが．．．

具体的なについての変分計算なら部分積分の前に変分が終わりますが，一般的なは偏微分という形で最後までのこってしまいますよね．

Re: ラグランジュの運動方程式

やかんさんのレス (2006/05/30(Tue) 11:45)

＞EL方程式で偏微分がややこしいのは，それが変分計算の名残だから，と思っているのですが．．．

変分，と考えると，なんかちょっと不思議な感じがなくなるような気がします．関数関係にある本来の変数値から，”その関係に関係なく”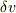， $\delta v$ だけ仮想的にずらすのだから（あるいは”ずれた”場合を考えるのだから）かまわないのだ，という事だからいいのかな．だんだん考えてるうちに，やっぱり単に独立変数と考えればそれでいいんだ！と納得できちゃいそうになりました．有難うございました．m(__)m

Re: ラグランジュの運動方程式

ｙama さんのレス (2006/06/05(Mon) 14:28)

やかんさんの疑問が気になったので，考えてみました．速度と座標を，初めは独立な変数として扱っているのに，最後に 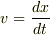$v=\frac{dx}{dt}$ の関係が決まるのが不思議だという疑問です．

toorisugari no Hiro さんは 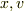x,v が独立に選べることについて

>軌道を忘れてしまえば，各時刻の「初期」条件のペアを別々に考えることができ，かつ，それぞれを独立にできます．

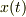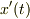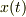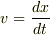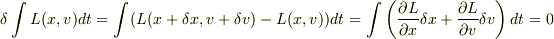と述べられています．ところが作用積分を計算するには，運動を考える全時間の x(t) を与えないといけません．その場合には速度 x'(t) も決まってしまって x(t) と独立に速度を選ぶ余地はなくなります．もし独立に選べば， $v=\frac{dx}{dt}$ の関係が成り立たなくなりますが，その場合，後になってこの関係ができてくる根拠が不明です．「軌道を忘れてしまえば」速度と座標を独立に選ぶことは可能かもしれませんが，そうすると運動方程式を導く際に問題が生じます． $\delta\int L(x,v)dt=\int (L(x+\delta x,v+\delta v)-L(x,v))dt=\int \left(\frac{\partial L}{\partial x}\delta x+\frac{\partial L}{\partial v}\delta v\right)dt=0$ となりますが，ここで 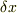$\delta x$ と $\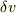delta v$ が完全に独立で任意の値をとれるとすれば， $\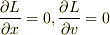frac{\partial L}{\partial x}=0,\frac{\partial L}{\partial v}=0$ でなければならなくなり，正しい運動方程式は得られません．もしここで， $\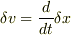delta v=\frac{d}{dt}\delta x$ という関係が成り立てば 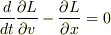$\frac{d}{dt}\frac{\partial L}{\partial v}-\frac{\partial L}{\partial x}=0$ が導かれますが，とが独立であるのに $\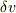delta v$ と $\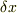delta x$ の間にこの関係がなりたつ根拠はありません．さらに， $\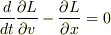frac{d}{dt}\frac{\partial L}{\partial v}-\frac{\partial L}{\partial x}=0$ が運動方程式になるためには $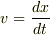v=\frac{dx}{dt}$ の関係が必要ですが，変分によってこの関係が導かれるわけではありません．これにたいして，初めから $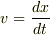v=\frac{dx}{dt}$ の関係がなりたっていると考えれば，当然 $\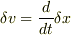delta v=\frac{d}{dt}\delta x$ も成り立つことになります．従って，ハミルトンの原理は，あくまでも座標の変化に対して作用積分の変分が0になるものと考えるのが正しいと思います．もちろん速度も変化しますが，それは座標の変化に付随するものであって，座標と全く独立に変化するのではないと思います．すなわち,ハミルトンの原理は $\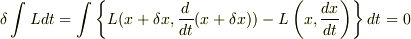delta\int Ldt=\int\left\{L(x+\delta x,\frac{d}{dt}(x+\delta x))-L\left(x,\frac{dx}{dt}\right)\right\}dt=0$ ということだと思います．実際，ラグランジアンが $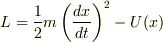L=\frac{1}{2}m\left(\frac{dx}{dt}\right)^2-U(x)$ の場合は, $\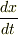frac{dx}{dt}$ による偏微分を行うことなくこの変分を計算することができて，その結果，運動方程式 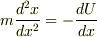$m\frac{d^2x}{dx^2}=-\frac{dU}{dx}$ が得られます．しかし，ラグランジアンの形が具体的に与えられていない一般的な場合には，変分の計算の過程で $\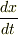frac{dx}{dt}$ による偏微分を行うことが必要になります．偏微分では，関数関係を無視してを定数と見なして $\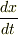frac{dx}{dt}$ で微分します．しかし偏微分の意味を考えれば，それは関数関係がないということではないと思います．

Re: ラグランジュの運動方程式

やかんさんのレス (2006/06/05(Mon) 16:32)

yamaさん，有難うございます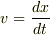． $v=\frac{dx}{dt}$ の関係がなくなるのではなくて，偏微分（微分ではなくて）というぐらいだから，関数関係を”無視して”，微分するという事なんですね．いろいろ教えていただいているうちに，納得できてきた気が致します．

Re: ラグランジュの運動方程式

toorisugari no Hiro さんのレス (2006/06/05(Mon) 23:46)

ｙamaさま

私の > 軌道を忘れてしまえば，各時刻の「初期」条件のペアを別々に考えることができ，かつ，それぞれを独立にできます．

はご指摘通り，おかしいです．スレッドの前半と後半で私の意見は矛盾しています．

「言葉が正確でなかったので書き直します．」のときに前半の考え方がおかしいのは自分でも気づいたのですが，考えをうまく整理できなかったことと，スレッドの流れで，訂正するタイミングを失っていました．

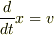$\frac{d}{dt}x=v$ の関係は最初から満たしている．偏微分は変分によるもので，そのときの「 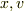x,v が独立」というのは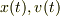， x(t),v(t) が独立な関数と言う意味ではなく，Lagrangian 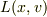L(x,v) の引き数が形式上独立にとれることにすぎない．

ということでいいでしょうか?

# どうも，off-shellという言葉を拡大解釈してたようです．

指摘いただきありがとうございます．

Re: ラグランジュの運動方程式

ｙama さんのレス (2006/06/06(Tue) 08:45)

そういうことでよろしいかと思います．このあたりのことは，私もあまりきちんと考えたことがなかったので，考え直してみる良い機会でした．

[home] [掲示板] [ページの先頭]