フーリエ解析の最小二乗法的性質
フーリエ解析の最小二乗法的性質
トンガリ さんの書込 (2006/05/22(Mon) 10:10)
以下に持論を勝手に述べる.皆様から様々な御指摘を頂けると幸いです.
1.このホームページの表題『最小二乗法』を拝見した.
表題『最小二乗法』での解説は,具体的には, 『最小二乗法を使って,測定データから実験式y=ax+bを得る方法』である.
表題『最小二乗法について』の『一般的な場合』の解説から,
『最小二乗法』は原理が簡単である割には,応用範囲が広いと確信した. 御免,よく観たら,広い意味での『最小二乗法』の解説ではなかった. 広い意味では,ウィキペディアの『最小二乗法』を参考にして下さい.
それはさて置き,
2.私が昔,摘まみ読みしたフーリエ解析の書物の3〜4冊の中に,ただ1冊にだけ, 『フーリエ解析は最小二乗法的性質を有する.』と一言だけ述べていた. 私は当時,この件について詳しく解説した書物があれば良いのにと思った.
3.『最小二乗法を使って,測定データから実験式y=aCOS(θ)を得る方法』 は珍規だが可能なはず.上記方法で導かれる,1次の余弦係数 a の計算式が, フーリエ解析の書物で導かれている1次のフーリエ余弦係数の計算式と, 仮に同一式であるならば, 機械設計者は『フーリエ解析は最小二乗法的性質を有する.』を信じてやっても良い.
4.『フーリエ解析は最小二乗法的性質を有する.』を本当に理解できた暁には, フーリエ解析に対する理解が,私にとっては雲が晴れるように拡大する気がする. 私にとって拡大の例は, 測定データのθが0〜360度に充実してない0〜70度の場合でもフーリエ解析できる. 測定データのθが例えば5度刻みの等間隔でなくてもフーリエ解析できる.
5.私は今後, 『最小二乗法を使って,測定データから実験式y=aCOS(θ)を得る方法』で, 1次の余弦係数 a の計算式を導く予定である. この掲示板に投稿するには,積分記号の表記方法を習得しなければなりせん. それがサイトマップの何処にあったか教えて下さい.
<次回に続く>
Re: フーリエ解析の最小二乗法的性質
CO さんのレス (2006/05/22(Mon) 11:31)
トンガリさん,こんにちは.
> この掲示板に投稿するには,積分記号の表記方法を習得しなければなりせん. > それがサイトマップの何処にあったか教えて下さい.
積分記号は日本語変換で「せきぶん」としても出てきますが,より綺麗に,正確に表現したいときは TeX 数式を使うことをお勧めします.以下のURLに,この掲示板における数式の扱い方が書いてありますので参考にしてください.
よろしくお願いいたします.
Re: フーリエ解析の最小二乗法的性質
トンガリ さんのレス (2006/05/22(Mon) 19:24)
『最小二乗法を使って,測定データから実験式y=aCOS(θ)を得る方法』で, 私が先に5.で述べた通り,1次の余弦係数aの計算式を以下に導かんとする.
6.測定データとして次のような数値の組の集合があったとする. {θ,y}={θ1,y1},{θ2,y2},...,{θn,yn} これら{θ,y}の分布がy=aCOS(θ)という関数に従うと仮定したとき,想定される理論値は, {θ1,aCOS(θ1)},{θ2,aCOS(θ2)},...,{θn,aCOS(θn)} ということになり,実際の測定値との残差は各iにつき|yi−aCOS(θi)|である. したがって,理論値からの誤差の分散は残差の平方和 i=1〜nのΣ {yi−aCOS(θi)}^2・・・・・【式1】で与えられる.
【式1】の値を最小にする係数aを求めるのが『最小二乗法』である.【式1】を展開すると, i=1〜nのΣ{yi−aCOS(θi)}^2= i=1〜nのΣ{(yi)^2−2yi*aCOS(θi)+a^2*(COS(θi))^2}= {i=1〜nのΣ(yi)^2}−{i=1〜nのΣ2yi*aCOS(θi)}+{i=1〜nのΣa^2*(COS(θi))^2}= {i=1〜nのΣ(yi)^2}−2a{i=1〜nのΣyi*COS(θi)}+a^2{i=1〜nのΣ(COS(θi))^2}・・・・・【式2】
【式2】の値を最小とする係数aを求めるために,【式2】を係数aで微分して 0 と置くと, −2{i=1〜nのΣyi*COS(θi)} +2a{i=1〜nのΣCOS(θi)^2}=0・・・・・【式3】,を整理して, a={i=1〜nのΣyi*COS(θi)}÷{i=1〜nのΣCOS(θi)^2} ・・・・・【式4】 【式4】被除数と除数に(1/n)を掛けて,更に半角の公式 COS(θi)^2=0.5(COS(2θi)+1)を代入して, a=(1/n){i=1〜nのΣyi*COS(θi)}÷(1/n){i=1〜nのΣ0.5(COS(2θi)+1)} ・・・・・【式5】
残念ながら,これにて私が式を整理できる限界に達した. a=(1/n){i=1〜nのΣ2yi*COS(θi)} ・・・・・【フーリエ解析の書物で導かれている1次のフーリエ余弦係数の式】
と似ているようで似てない.かといって【式5】が誤りとは断定できない. 7.そこで,やむを得ず私の前言 >測定データのθが0〜360度に充実してない0〜70度の場合でもフーリエ解析できる. >測定データのθが例えば5度刻みの等間隔でなくてもフーリエ解析できる. を取り消すと言うか,一旦は無き物にさせて頂きます.
そうすると,i=1〜nの集合 {θ}={θ1},{θ2},,...,{θn}が 例えばn=72で,{θ1}=0度,{θ2}=5度,...,{θ72}=355度の全区間の場合と, 例えばn=36で,{θ1}=0度,{θ2}=5度,...,{θ36}=175度の半区間の場合は, 【式5】の除数部分は (1/n){i=1〜nのΣ0.5(COS(2θi)+1)}=0.5 ・・・・・【式6】,と算出されるのは明白である. 【式6】を【式5】に代入すると,目出度く大願成就で,
a=(1/n){i=1〜nのΣ2yi*COS(θi)} ・・・・・【式7】(ただしnを全区間または半区間に限定した場合) を得た. 8.フーリエ級数の書物では全区間と半区間のフーリエ展開しか扱ってないので,それしか無いのか知らん. だとすれば,私が先に3.で述べた通り, 『最小二乗法を使って,測定データから実験式y=aCOS(θ)を得る方法』で導かれた1次の余弦係数aの 計算式【式7】は【フーリエ解析の書物で導かれている1次のフーリエ余弦係数の式】と同一式であるので, 機械設計者は『フーリエ解析は最小二乗法的性質を有する.』を信じるに至った. 9.『最小二乗法を使って,測定データから実験式y=aCOS(θ)を得る方法』の結論の【式5】は正しい. >測定データのθが0〜360度に充実してない0〜70度の場合でもフーリエ解析できる. >測定データのθが例えば5度刻みの等間隔でなくてもフーリエ解析できる. を取り消したと言うか,一旦は無き物にしたものの,何か工夫して有効利用できないかと私は迷っている.
Re: フーリエ解析の最小二乗法的性質
トンガリ さんのレス (2006/05/22(Mon) 21:23)
私は先に9.で 『最小二乗法を使って,測定データから実験式y=aCOS(θ)を得る方法』 の結論である1次の余弦係数aの計算式 a=(1/n){i=1〜nのΣyi*COS(θi)}÷(1/n){i=1〜nのΣ0.5(COS(2θi)+1)} ・・・・・【式5】 は正しいと述べた.
私の直感ではあるが,以下の私の解釈は言い過ぎであろうか.
10.『最小二乗法を使って,測定データから実験式y=aCOS(θ)を得る方法』で導かれた【式5】が普遍的であって, 【 フーリエ解析の書物で導かれている1次のフーリエ余弦係数の式】は全区間または半区間の特異な例である.
証明もできない機械設計者が,偉そうに勝手に申してすみませんでした.
Re: フーリエ解析の最小二乗法的性質
トンガリ さんのレス (2006/05/24(Wed) 18:49)
私は先に9.で 『最小二乗法を使って,測定データから実験式y=aCOS(θ)を得る方法』 の結論である1次の余弦係数aの計算式 a=(1/n){i=1〜nのΣyi*COS(θi)}÷(1/n){i=1〜nのΣ0.5(COS(2θi)+1)} ・・・【式5】を得た.
10.【式5】の除数部分 (1/n){i=1〜nのΣ0.5(COS(2θi)+1)} は nの値が十分大きいと仮定して,言い換えれば,θn/nの値が十分小さいと仮定して, 区間積分 (1/θn){θ=0〜θnの∫0.5(COS(2θ)+1)*dθ}・・・・・【式A】で表される. 区間積分 (1/θn){θ=0〜θnの∫COS(θ)^2*dθ}・・・・・・・・・【式B】で表しても良い. これらの区間積分を解くと,0.5+0.25COS(2θn)/θn ・・・【式C】であった. 【式C】にはCPUで数値計算する場合に計算時間を短縮する効果がある.
11.したがって,【式5】を下記の形式で表現しても良い. a=(1/n){i=1〜nのΣyi*COS(θi)}÷(1/θn){θ=0〜θnの∫0.5(COS(2θ)+1)*dθ} ・・・【式5A】 a=(1/n){i=1〜nのΣyi*COS(θi)}÷(1/θn){θ=0〜θnの∫COS(θ)^2*d} ・・・・・・・・・【式5B】 a=(1/n){i=1〜nのΣyi*COS(θi)}÷{0.5+0.25COS(2θn)/θn} ・・・・・・・・・・・・・・【式5C】
【式A】または【式B】または【式C】のグラフは, 値が1で始まり最終的には0.5に収束する周期πの減衰振動曲線に似ている.具体的な値を以下に示す.
θn=0のときの値は 1 θn=(1/4)πのときの値も 0.5 θn=(128.7/180)πのときの値は 0.3914 (谷の極値) θn=πのときの値は 0.5 (半区間フーリエ展開の区間に相当する.) θn=(221.3/180)πのときの値は 0.5642 (山の極値) θn=(3/4)πのときの値も 0.5 θn=(312.4/180)πのときの値は 0.4543 (谷の極値) θn=2πのときの値は 0.5 (全区間フーリエ展開の区間に相当する.)
【式A】または【式B】または【式C】が明示されたことで, 持論のフーリエ解析に留まらず,フーリエ級数の考察に発展する足掛かりを得た気がする.
以上にて私の持論の発表を終わります.ご査読下さいます様お願い致します.
Re: フーリエ解析の最小二乗法的性質
toorisugari no Hiro さんのレス (2006/05/24(Wed) 22:44)
詳しく文を読んだ訳でないので文に対する意見は避けさせてもらいます. 一般論だけ.
データに誤差はないを前提としたとき,最小二乗法的考え方(というよりガラーキン法ですね.)を使われるなら,点の個数と同じ自由度のモードの和で考えないと一般には無意味です.
つまり  から
から 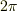 の区間で,
の区間で, 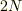 個の点のデータ(不等間隔でも良い)からフーリエ成分を計算されたいのなら,
個の点のデータ(不等間隔でも良い)からフーリエ成分を計算されたいのなら, 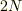 個のモード(
個のモード( 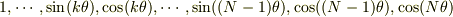 )で作った「多項式」で近似しないと意味は有りません.
)で作った「多項式」で近似しないと意味は有りません. 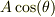 のみでfittingしようとしても正しいデータはえられません.(等間隔のときは「偶然」うまくいきます.)
のみでfittingしようとしても正しいデータはえられません.(等間隔のときは「偶然」うまくいきます.)
例として区間 ![[x_0,x_1]](http://hooktail.maxwell.jp/bbslog/beffd3be5baa5d06164c7401af76b3ff.png) において,
において, 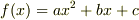 に対して
に対して 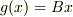 で
で
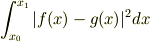
を最小にするようにfittingする事を考えましょう.
計算すればわかりますが, 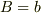 に一般にはなりません.(
に一般にはなりません.( 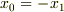 のときには「偶然」成立しますが.)任意の区間で正しい答えがでるようにしたいのなら,
のときには「偶然」成立しますが.)任意の区間で正しい答えがでるようにしたいのなら, 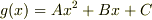 と仮定して計算しなければいけません.
と仮定して計算しなければいけません.
話を三角関数に戻すと,不等間隔のときは点の個数と同じ個数のモードの和でfitting することで計算は可能ですが, 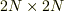 の行列の逆行列計算が必要でとても大変です(等間隔のときは「偶然」逆行列計算は不要になりますが).しかも誤差に敏感ですから実用になるとは思えません.
の行列の逆行列計算が必要でとても大変です(等間隔のときは「偶然」逆行列計算は不要になりますが).しかも誤差に敏感ですから実用になるとは思えません.
Re: フーリエ解析の最小二乗法的性質
トンガリ さんのレス (2006/05/25(Thu) 00:53)
先に一旦終了宣言をしましたが, 1次の余弦係数aのみについて述べて,1次の正弦係数bについて全く述べてないのは片手落ちであるので, 以下に1次の正弦係数bについて簡単に述べる.
話を簡単明快にするため,ここでは終始,1次の係数a,bについてのみ説明する事になりますが, 任意の次数の係数a,bについては容易に類推できるはずです.(フーリエ級数の書物を参考にして下さい) フーリエ解析では,次数ごとに係数a,bを求めます.他の次数の係数a,bとは無関係に求めるのです. 『最小二乗法』を使って任意の次数の係数a,bを求める場合も,他の次数に対して独立だと,私は直感する. フーリエ合成では,任意の次数の合成の後に,これに他の次数を追加する時は,単純に加算するのです.
12.『最小二乗法を使って,測定データから実験式y=bSIN(θ)を得る方法』で私が導いた, 1次の正弦係数bは以下の【式】で表される. b=(1/n){i=1〜nのΣyi*SIN(θi)}÷(1/n){i=1〜nのΣ0.5(−COS(2θi)+1)} ・・・・・【正弦式5】 b=(1/n){i=1〜nのΣyi*SIN(θi)}÷(1/θn){θ=0〜θnの∫0.5(−COS(2θ)+1)*dθ} ・・・【正弦式5A】 b=(1/n){i=1〜nのΣyi*SIN(θi)}÷(1/θn){θ=0〜θnの∫SIN(θ)^2*dθ} ・・・・・・・・・【正弦式5B】 b=(1/n){i=1〜nのΣyi*SIN(θi)}÷{0.5−0.25COS(2θn)/θn} ・・・・・・・・・・・・・・【正弦式5C】
13.【正弦式5C】の除数部分 {0.5−0.25COS(2θn)/θn} は 前に述べた【5C】の除数部分に対して,【正弦式5C】の除数部分=1−【5C】の除数部分 の関係にある. 【正弦式5C】の除数部分のグラフは, 値が0で始まり最終的には0.5に収束する周期πの減衰振動曲線に似ている.具体的な値を以下に示す.
θn=0のときの値は 0 θn=(1/4)πのときの値も 0.5 θn=(128.7/180)πのときの値は 0.6086 (山の極値) θn=πのときの値は 0.5 (半区間フーリエ展開の区間に相当する.) θn=(221.3/180)πのときの値は 0.4358 (谷の極値) θn=(3/4)πのときの値も 0.5 θn=(312.4/180)πのときの値は 0.5457 (山の極値) θn=2πのときの値は 0.5 (全区間フーリエ展開の区間に相当する.)
したがって,【正弦式5C】の除数部分を0.5としたとき, b=(1/n){i=1〜nのΣ2yi*SIN(θi)} ・・・・・【正弦式7】(ただしnを全区間または半区間に限定した場合) この式は?フーリエ解析の書物で導かれている1次のフーリエ正弦係数の式?と寸分違わぬ同じ式である.
Re: フーリエ解析の最小二乗法的性質
トンガリ さんのレス (2006/05/25(Thu) 08:31)
Excelで計算してみて,【通りすがりの人】のご指摘通り,私の考えは間違いと判明した. Excelでの計算はθ=5度から70度まで5度刻みの測定データ y=1+2COS(θ)+3COS(2θ)で行った.
奇関数とは限らない一般的な計測データでは,全区間のフーリエ解析でないと,実行困難と分かった. A.測定データのθが0〜360度に充実してない0〜70度の場合でもフーリエ解析できる. B.測定データのθが例えば5度刻みの等間隔でなくてもフーリエ解析できる. と,私が夢見たことは私には到底出来ない.連立方程式が苦手な私の力では出来ないと分かった.
私が昔,摘まみ読みしたフーリエ解析の書物の3〜4冊の中に,ただ1冊にだけ, 『フーリエ解析は最小二乗法的性質を有する.』と一言だけ述べていた. の件での私の理解の進展は,以下の結論とする.
C.一般的な測定データでの全区間のフーリエ解析のときに限って, 任意次数のフーリエ係数の計算式は『最小二乗法』を使って任意次数ごとに導いた式と意味不明ながら同一である.
D.a=(1/n){i=1〜nのΣ2yi*COS(θi)} ・・・【フーリエ解析の書物で導かれている1次のフーリエ余弦係数の式】 でyi*COS(θi)を2倍する必然性を,『最小二乗法』を使って他方面から納得しただけである.大分徒労であった. 全区間のフーリエ解析であれば,周波数の異なる成分が積和で相殺されて,計算結果が0になるのが妙手だった.
Re: フーリエ解析の最小二乗法的性質
toorisugari no Hiro さんのレス (2006/05/25(Thu) 14:57)
> A.測定データのθが0〜360度に充実してない0〜70度の場合でもフーリエ解析できる. > B.測定データのθが例えば5度刻みの等間隔でなくてもフーリエ解析できる.
BはもちろんAも可能です.ただし,0から70度のデータ(離散データとします)に加えて,360度のデータが0度のデータと等しいことが「保証」されているならです.そしてデータの個数だけのモードを使って計算すれば,これは不等間隔データを用いたことに等しく,結果70度から360度まで「補間」をすることになります.
もちろん正確に360度の周期関数であることが前もって保証されていないと,全くのナンセンスですし,保証されていても,前にふれましたが,計算量・精度の観点から おすすめできる方法ではないです.