とし さんの書込 (2006/05/18(Thu) 18:02)

はじめまして．大学の理学系学部１年のとしです． 物理はあまり得意ではないですが，よろしくお願いします．

力学でわからない所があったので質問させていただきます．

半径Ｒの滑らかな球面の頂点に質量ｍの物体をのせ， ｔ＝０で初速度ｖを与えて滑らせたとき， 物体の滑った距離をｓとしてｓについての運動方程式を立て， ｓ＝ｓ（ｔ）をｔの３次までの近似で求めよ． （ただし重力をｇとし，空気抵抗は無視する）

ｓについての運動方程式が m*(d^2s/dt^2) = mgsin(s/R) になると思うんですが，とりあえずｓ（ｔ）を ｖｔ＋ａｔ^2＋ｂｔ^3とおいて運動方程式に代入し， 初期条件からａ＝０が導き出せたのですが，ｂがなかなか出てきません． 色々やっているうちにわけがわからなくなってしまいました． 着目する部分を間違えているのでしょうか・・

よろしくお願いします．

Joh さんのレス (2006/05/18(Thu) 18:11)

運動方程式を解いてから，sinを級数展開したらどうでしょうか．

とし さんのレス (2006/05/18(Thu) 18:48)

この場合，運動方程式はどのように解いたらいいんでしょうか？ まだ習い始めなので，微分方程式も詳しくないもので・・・ たびたびすいません．

Joh さんのレス (2006/05/18(Thu) 19:42)

角度をうまいこと時間と関係づけられますか？

Joh さんのレス (2006/05/18(Thu) 20:09)

あれ，そんなことしなくていいのかな？そのままsinを級数展開して，最初の何項かだけ残せばいいんですかね．境界条件は，何と何を考えましたか？

とし さんのレス (2006/05/18(Thu) 20:45)

境界条件，とはどういうことでしょうか．．

Joh さんのレス (2006/05/18(Thu) 21:33)

微分方程式を解くとき定数を決めるのに必要な初期条件や端点条件のことです

とし さんのレス (2006/05/18(Thu) 21:41)

ｔ＝０の時に初速度ｖを与える（つまり加速度もｔ＝０で０ですよね） ということしかわかっていないんですが，不十分なんでしょうか． 問題文には 「時刻ｔ＝０にスタートした直後，距離ｓ＝ｓ（ｔ）はどのように増えるか． ｔについての３次までの近似で求めよ．」と書いてありました．

級数展開必要なんでしょうか．

トンガリ さんのレス (2006/05/18(Thu) 21:59)

一つだけ言わせて．

頂点の傾斜は水平方向なので，初速度ｖが水平方向であるに違いない． 滑らせるからには，物体が球面を離れて空中に飛ばないための条件は， 頂点での半径Ｒの円運動に必要な向心加速度＝＜重力加速度ｇ ｖ^2÷Ｒ＝＜ｇ，すなわち，ｖ＝＜SQRT(Ｒｇ) が必須条件である．

この結論に至る前には，勿論， 水平方向初速度ｖの自由落下の位置のグラフと円弧を思い浮かべた．

Joh さんのレス (2006/05/18(Thu) 22:31)

すみません．さっきまで，あまり考えずに書き込んでました．意外と難しいですね^^（汗）

いま，ちょこっと手元の紙に計算してみたんですが，間違えてたら教えて下さい． まず，基本の式はこうですか？

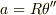
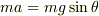
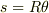
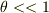
最初の二つから 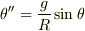が出てくるので，これを解いて 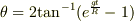となったんですが，これはいいですかねぇ．これを級数展開してＲを掛けて最初の三項取ればいいと思うんですが，どうでしょう．あんまり計算に自身がないんでどっか間違えてないか一緒に考えて下さい．なんか検算するのも嫌な結果です．

とし さんのレス (2006/05/18(Thu) 22:50)

トンガリさん，Johさん，ありがとうございました． 今からやってみますが，見た感じではそれでいいと思います． 僕も計算には自身がないのでなんどか試してみます． ありがとうございました．m(_ _)m

Joh さんのレス (2006/05/18(Thu) 23:00)

いや，たぶん積分まちがえました．もう一回気持ちを落ち着けて計算してみますね．としさんも分かったら教えて下さい．

yama さんのレス (2006/05/19(Fri) 00:42)

私からも一言． 初速度が速過ぎれば初めから空中に飛び出すし，遅くても途中で球面から離れます． しかし，球面上を運動している範囲に限ると，その運動は単振り子の運動と同じになります．といっても往復運動ではなく，円運動をする場合です． すなわち，伸び縮みしない軽い棒におもりをつけて支点からつるし，最下点でおもりに初速度を与えて運動させるとします．初速度が小さければ往復運動になりますが，初速度が大きい場合は最高点を通過して円運動をします． この最高点付近の運動が，問題となっている球面上の運動と同じになるわけです． このような単振り子の運動は，大抵の力学の教科書に載っていますが，エネルギーの積分を利用して，楕円関数で表すことができます． しかし，この問題の場合は運動方程式を解かなくても，Johさんが言われるように sinθ を t の級数に展開して，運動方程式の両辺の係数を比較すればいいと思います．

とし さんのレス (2006/05/19(Fri) 02:11)

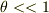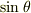この状態で より を で近似してしまうというのはどうなんでしょうか． 高校の時の単振り子ではそのような近似を使った覚えがあるんですが．

Joh さんのレス (2006/05/19(Fri) 02:22)

それでは一次なので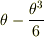， で近似してみてください．

Joh さんのレス (2006/05/19(Fri) 06:05)

混乱させてすみません．θの一次近似でいいんですね．そうするとθが双曲線関数で求まるので，その近似の最初の三項を取ればいいんですね．どうも，tの関数としてのθの近似というのと，サインの近似というのを途中から私が混乱しました．

トンガリ さんのレス (2006/05/19(Fri) 09:54)

yamaさんの一言をヒントに， 途中で球面から離れる角度Θの余弦，COS(Θ) 即ち COS(s／R) を下記に求めた．

エネルギー保存の法則から， 0.5m(sの速度)^2＝0.5mv^2＋mgR(1−COS(s／R)) 整理して， (sの速度)^2＝v^2＋2gR(1−COS(s／R)) さらに， (sの速度)^2／R＝(v^2＋2gR(1−COS(s／R))）／R 上記の両辺は共に向心加速度を表わす．

このときの重力加速度の球面に垂直な成分は g・COS(s／R) である． 【 途中で球面から離れる瞬間の条件は 】 g・COS(s／R) ＝ (v^2＋2gR(1−COS(s／R))）／R

両辺にRを掛けて， gR・COS(s／R) ＝ v^2＋2gR(1−COS(s／R)) 整理して， 3gR・COS(s／R) ＝ v^2＋2gR ゆえに， 【 COS(s／R) ＝ v^2／3gR＋2／3 】 を得た．

ちなみに，初速度v＝0 のとき，COS(s／R) ＝ 2／3 だから， Θ＝48.2度，換言すれば，s／R＝0.841[ラジアン] で球面から離れる． 直径115mmの研磨鋼円柱上を直径8mmの研磨鋼球を落下させる実験で，正解の内と確認した． 決して，Θ＝Θ0度のデタラメや，Θ＝80度と誤読する角度にはならない．

頂点で球面から離れる初速度を検算すると，1 ＝ v^2／3gR＋2／3 だから， v ＝ SQRT(gR) で私の前言に合っている．

機械設計者の立場では，円弧から離れる角度と速度が解れば十分で，離れるまでの 時間的経過に実用的価値はない．離れる時刻を知らなくても，X-Yのグラフは描ける． 普通は，円弧上にあるときの s＝vt＋at^2＋bt^3 かの a，b を求める努力はしない．

ｙama さんのレス (2006/05/19(Fri) 10:00)

Johさんの解きかたでいいと思います． 別の解き方として，運動方程式を解いてから近似するのではなく，ｓ（ｔ）＝ｖｔ＋ａｔ^2＋ｂｔ^3 を直接運動方程式に代入して，両辺の係数を比較してもいいと思います． この場合，運動方程式の左辺は ｔ の1次式になるので，右辺も ｔ の1次式で近似すればよいことになります． 従って，右辺＝mgsin(s/R)≒mgs/R≒mgvt/R となるので，左辺との係数比較によってａ，ｂ が求められます．

とし さんのレス (2006/05/20(Sat) 00:13)

返信遅れてすみません．返信してくれた方ありがとうございます． やはり 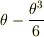で代入して積分するといい感じにでてきました． もう一度自分でがんばってみようと思います．

ありがとうございました．m(_ _)m