シュレディンガー
シュレディンガー
芹菜 さんの書込 (2006/05/16(Tue) 23:32)
はじめまして,芹菜といいます. 大学で物理を勉強しています.
時間を含まない3次元自由粒子に対するシュレディンガー方程式の解が,
Ψ(x,y,z)= 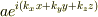 となることを示す問題がありました.
となることを示す問題がありました.
波動方程式は,
Φ( 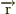 ,t)=Ψ(x,y,z)・
,t)=Ψ(x,y,z)・ 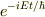 となると考えます.
となると考えます.
シュレディンガー方程式を変形して,
k= ![\frac{\sqrt[2]{\mathstrut 2m(V-E)}}{\hbar}](http://hooktail.maxwell.jp/bbslog/e625171d05a30a637c1260410a25dec9.png) とおいて,
解を
とおいて,
解を 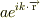 と考えたのですが,これでは示せていないと思います.
と考えたのですが,これでは示せていないと思います.
どうすれば正しく考えられますか?教えてください.
Re: シュレディンガー
yama さんのレス (2006/05/17(Wed) 09:35)
自由粒子だから V=0 なので,時間を含まないシュレーディンガー方程式は
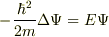 となります.
Ψ(x,y,z)=X(x)Y(y)Z(z) と置いて両辺を XYZ で割れば変数分離できます.
となります.
Ψ(x,y,z)=X(x)Y(y)Z(z) と置いて両辺を XYZ で割れば変数分離できます.
Re: シュレディンガー
芹菜 さんのレス (2006/05/17(Wed) 20:05)
返信ありがとうございます. 計算してみました.
代入したあと両辺をXYZで割ると,
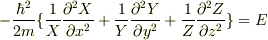
となり,各成分において
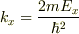
と置いていって,解が求まる.
という考えで間違ってないでしょうか?
Re: シュレディンガー
yama さんのレス (2006/05/17(Wed) 22:49)
X,Y,Z はそれぞれ1変数の関数なので,偏微分ではなく常微分になります.
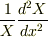 は定数でなければならないので
は定数でなければならないので
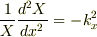 などと置くと
などと置くと
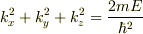 が成り立つことになります.
が成り立つことになります.
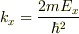 > と置いていって,解が求まる.
> と置いていって,解が求まる.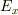 って何でしょう?
って何でしょう?