リサージュ図形の方程式の求め方

タスクさんの書込 (2006/05/09(Tue) 14:13)

初めて投稿させていただきます，大学生のタスクと申します．よろしくお願いします．

題は位相角が90度で,周波数比が1:1,1:2,1:3の三つの図形がある．この三つの図形の方程式を求めよです．

関数f(x,y)=0を使って解けばよいみたいですが，どのように導くのかさっぱりわかりません．教えてください．

こんにちは，タスクさん．

まずは > 位相角が90度で,周波数比が1:1,1:2,1:3 これを数式化してみてはどうでしょうか．

また，物理のかぎしっぽにもリサージュ図形の記事がありますので，目を通してみると良いと思います．

返信ありがとうござます．この記事は一度読んだのですが，どのように f(x,y)=0 を使うのかがわかりませんでした．

タスクさん，こんばんは．

> どのようにf(x,y)=0 を使うのか

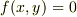f(x,y)=0 を使うんですか？結果的に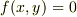の形の方程式を導くということではないでしょうか？ (・・?

>>結果的にの形の方程式を導くということではないでしょうか？そうです．そうなんだと思います．しかし結局どうするのかわかりませんでした．

> しかし結局どうするのかわかりませんでした．

それでは，まずは周波数比 1:1 の場合を考えてみてはどうでしょうか．

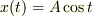$x(t) = A \cos t$ とおきます．位相が 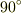$90^{\circ}$ ずれていることより $y(t) = B \cos(t-90^{\circ}) = B \sin t$ となります．

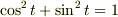$\cos^2 t + \sin^2 t = 1$ という関係があるので・・・

これで 1:1 の場合はできませんかね？

ええ〜とつまり cost=x/Aと置きまして． y^2=B^2sin^2t^2=B^2(1-cos^2t)=B^2-B^2cos~2t y^2=B^2-B^2(x/A)^2 でいいのでしょうか？

ええ，良いのではないでしょうか．ただ，

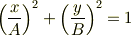
$\left(\frac{x}{A}\right)^2 + \left(\frac{y}{B}\right)^2 = 1$

という形のほうが分かりやすいかな，と．この式が何を表しているかはわかりますよね？

1:2, 1:3 の周波数比についても，とりあえず条件を数式化してみれば先が見えると思います．

ありがとうございました．おかげで問題を解くことができました．

良かったです．またなにかあればどうぞ :)