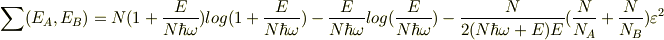統計力学
統計力学
たじゅ さんの書込 (2006/05/04(Thu) 01:16)
はじめまして,大学の物理学科で勉強中のたじゅです. 岩波の基礎物理シリーズ?統計力学という本を読んでいたのですが,数学的な知識が追いつかず,式が追えない部分があります.どうかご助力ください.
本ではp.16あたりなのですが.
二つの固体A(原子数 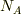 ),B(原子数
),B(原子数 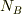 )が接触しているモデルのエネルギー配分の確率を考える.
各エネルギーが,
)が接触しているモデルのエネルギー配分の確率を考える.
各エネルギーが, 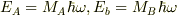 となる確率は,
となる確率は,
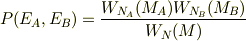
この確率を最大にする状態を求める.分母は一定より,分子について考察.
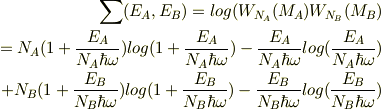
この確率が最大になる 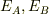 からわずかにずれた状態,
からわずかにずれた状態,
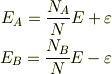
とおき,εにつき展開し二次の項までとると,

となる.
と記述されているのですが,展開後の式へたどり着けません. テイラー展開をするのだと思い,公式を見ながらやろうとおもったのですが, どう応用してよいかうまくいかず分からなくなりました. 一部の計算過程だけでもよいので,どなたか過程を示してくださるとほんとうに助かります.
さらに,この関連で, 体積Vの容器にN個の気体分子をいれたとき,分子の密度が場所に寄らず一様になることはどのようにして示したらよいのでしょうか?
この二点について回答をしていただきたく思います. 瑣末な質問だとは思いますが,よろしくお願いします.
Re: 統計力学
たじゅ さんのレス (2006/05/04(Thu) 01:28)
たびたびすみません. 上記の式の形すべてにミスなのですが,はじめのN(〜)…っていうところなんですが, N{(…)log(…)−log(…)}−… というふうに大きなカッコでくくられるのでるが,うまく表示できませんでした. 分かりにくくなって申し訳ありませんが,どうかご回答ください.
本では同等の式がきれいな形で,16ページにのってます.
Re: 統計力学
yama さんのレス (2006/05/05(Fri) 10:15)
?(E A ,E B ) を ε の関数として ?(E A ,E B )=?(ε)=?(0)+?'(0)ε+(?"(0)/2)ε^2+・・・ のように展開するだけです. 定数をa,b,cなどに適当に置き換えて ?(ε)=N A {(1+c+aε)log(1+c+aε)-(c+aε)log(c+aε)}+N B {(1+c-bε)log(1+c-bε)+(c-bε)log(c-bε)} という形にしておくと計算が見通しよくなると思います.
分子の密度についても同じように考えることができると思います. 容器を2つの部分に分けて,それぞれの体積に比例して分布したときの分子数をN A , N B として,分子数が N A +ε, N B -ε である場合を考えるわけです.
Re: 統計力学
たじゅ さんのレス (2006/05/10(Wed) 13:46)
yamaさん,レスありがとうございます. 初めの展開は理解できました.
分子密度のことですが,書き込みを読んで自分なりに考えてみました. 全体の体積をV,そのなかにある小さな領域の体積をvとして,全体の分子数をN,小さな領域内にいる分子数をnと仮定しました.
n個の粒子が小さな領域の中にいる確率を,
v<<V,n<<Nのときの近似,
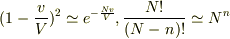 を使って,
を使って,
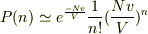 と求めてみました.
と求めてみました.
しかしここでこの先の考察ができなくなりました.
yamaさんの記述での 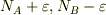 とするあたりです.
とするあたりです.
このままの議論でこの先どう考えたらよいのか,教えてください.よろしくお願いします. またこの確率を求める考察が間違っている場合,このままでは先に行き詰まる可能性がある場合もご指摘をお願いします.
Re: 統計力学
yama さんのレス (2006/05/10(Wed) 23:39)
P(n) の式はそれでいいと思います. 次に logP(n) をスターリングの公式などを用いて簡単な式で近似します. その式で,n=(v/V)N−ε と置いてから ε の巾級数に展開します. 当然ながら,1次の係数は 0 になり,a,b を定数として logP(n)=a−bε^2+・・・ の形になります. これから P(n) は ε=0 で最大になることが分かります. ε=0 ということは n/v=N/V ,すなわち分子数密度が全体平均の分子数密度に等しいということです. ε は,確率が最大となる粒子数からのずれですが,分子数密度のずれ ε/v について考えるために logP(n)=a−c(ε/v)^2+・・・ の形に書き換えると,係数 c は v に比例して大きくなることが分かります. このことは,v が大きくなるほど分子数密度の確率分布が最大値近傍に集中すること,すなわち密度のゆらぎが小さくなることを示しています.