球面調和関数
球面調和関数
ochi さんの書込 (2006/04/17(Mon) 21:28)
情報系大学院一年のochiと申します．
球面調和関数について質問があります． 勉強している目的はコンピュータグラフィックス，コンピュータビジョンでの利用のためです．（参考） http://www.hci.iis.u-tokyo.ac.jp/~okabe/cvim134_cr.pdf
自分で調べたところ球面調和関数は現在の物理学では量子力学で主に勉強するようだということはわかりました．そして極座標に変換したシュレディンガーの方程式を用いた水素原子の波動関数の解であるということはわかりました．
しかし数式の物理的意味(？)がわかりません．
ある本では「単位球面上のなめらかな関数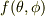 
は球面関数で展開できる」とありました．
ここからわかったことはフーリエ展開が正弦波の重ね合わせで関数を展開できるように何かしらの関数を球面調和関数というもので展開できるということです．
やはりここでも球面調和関数の意味がわからないため困ってしまいました．
直接この質問の回答でなくても何か参考になる資料など教えていただけたらありがたいです．
よろしくお願いします．
Re: 球面調和関数
山旅人 さんのレス (2006/04/22(Sat) 14:53)
ochi さん，初めまして．山旅人と申します．お尋ねの回答にはなっていないかもしれませんが…
> 球面調和関数の意味がわからないため困ってしまいました．
球面調和関数とは，数学的に厳密に定義された概念のひとつの表式でしょう． ですから，球面調和関数自体に意味があるのではなく，球面調和関数を用いて表された波動関数に球面調和関数の性質から演繹される意味が付与される，と私は考えます．と同時に，それを分析・考察する数学的な手段が付与される，と考えます． デジタル通信の可能性が，パルス波のフーリエ級数展開で理論的根拠を与えられたように．
Re: 球面調和関数
CB さんのレス (2006/04/23(Sun) 02:06)
はじめましてochiさん
>球面調和関数は現在の物理学では量子力学で主に勉強する・・ （単位科目としての）量子力学において，球面調和関数自体の議論はやらないです． ほとんどの量子力学の教科書では下のような流れで天下り的に「水素原子モデルの波動関数は球面調和関数となる」と導きます．
?水素原子モデルのポテンシャルが球対称であることから，球座標のシュレーディンガー方程式をたてる． ?変数分離をすると，半径方向と角度変数の微分方程式に分離できる． ?角度変数の微分方程式を初期条件などを考えて解いていくと，最終的に球面調和関数を求めることになる． ?水素原子モデルの電子の模型的空間的な分布は球面調和関数となる．（半径方向の関数との積）
球面調和関数自体の定義は検索すればいろいろと出てきますね．
とか
物理的な意味は方位量子数などをキーワードにして検索してみてはどうでしょうか
Re: 球面調和関数
ochi さんのレス (2006/04/24(Mon) 00:28)
山旅人さん，CBさんご回答ありがとうございます！！
>山旅人さん おっしゃりたい意図がわかりました．特に >球面調和関数自体に意味があるのではなく，球面調和関数を用いて表された波動関数に球面調和関数の性質から演繹される意味が付与される というところが納得です．
>CBさん 確かに多くの量子力学の本でそのように天下り的に書いてありました．
>物理的な意味は方位量子数などをキーワードに 早速調べてみたいと思います．
