ken さんの書込 (2006/04/15(Sat) 14:11)

kenです．掲示板に投稿するのは久しぶりです． 新社会人になられた崎間さん，他おめでとうございます． 私はもう社会人11年生になってしまいました． 満１０年をすぎてもぜんぜん成長していません．

今日はあるページ（後日明示するでしょうが今は伏せておきます） にこんな意味の記述をみました． （趣味で見ただけなので仕事とはまったく関係ありません． 仮にわからないままでも，なにも困ることはないのですが 気になっています）

点Oを中心とする直径（1+a）の円を描く． 点Oを通る直線を描き，上記円との交点をA,Bとする． A,B間を1:aに分割する点をCとする． 点Cから線ABに垂直な線を引き円との交点をD,D'とする． このとき点Cと点Dの間の長さは√aになる．

というものです． 最後の点Cと点Dの間の長さを求めようと作図してみたりしたのですが， 答えだけは√aと載っているのですが，なぜそうなるのかがわかりません． ヒントをおねがいします．

yama さんのレス (2006/04/15(Sat) 15:47)

AC＝１，BC＝a になることはすぐわかると思います． あとは，△ADCと△DBCの相似関係を利用しましょう．

ken さんのレス (2006/04/15(Sat) 17:34)

kenです．

yamaさんありがとうございました．

＞あとは，△ADCと△DBCの相似関係を利用しましょう．

△ADCと△DBCの相似関係に気づけばすぐわかりました． ABが円の直径だから，角ADBが直角になるのですね． （これに気づかなかったので相似だと思っていませんでした．） そのおかげで△ADCと△DBCが相似になる．（角度がすべて同じ） 後は辺の比をとる．

なお，もとのページは

• http://www12.plala.or.jp/ksp/algebra/Descartes/

で，その図２が気になっていたところでした． ああ，私が勝手に割り振ったAD,BDに線が引いてあって， 角ADBと点Cに直角記号が入っていればすぐに気づいたのだろうけれど．

やかん さんのレス (2006/04/15(Sat) 19:45)

kenさん，yamaさん，こんにちは！ 相似が思いつかなくても（私も思いつかなかった (^^;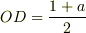） （円の半径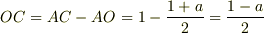） 三角形ODCは条件より直角三角形だから，三平方の定理を使って 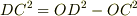に上記の値を代入してもいいかもしれませんね :)

ken さんのレス (2006/04/15(Sat) 22:13)

やかんさんこんばんわ >三平方の定理を使って 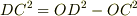に上記の値を代入してもいいかもしれませんね

なるほど，その手もありましたね． どちらを使っても，中学卒業レベルで解ける内容でした． どうやら自分の頭は固くなっていたようです．(^^;