sanga さんの書込 (2006/04/14(Fri) 12:40)

はじめまして．量子化学系の大学院生です． 量子力学の知識が不足していると感じ，最近勉強をはじめたのですが，以前から物理学のスタンスに対して気になっていることがありましたので，書き込みさせていただきました．お時間ありましたら，返信頂けるとうれしいです．

物理学では，基礎方程式(Newton's eq. Shrodinger's eq.など)を公理としていますが，自然現象とその解の対応関係はどのようになっているのでしょうか．つまり，基礎方程式の解はひとつではなく，複数の解(ベクトル，スカラー，関数)の集合から成り立っている一方，自然現象というものは一つの状態であるはずです．基礎方程式の解集合のなかで，自然現象に妥当な一つ(特解)をとりだしてくるととらえて構わないのでしょうか．

またこれに絡んだ話ですが，Newton's eq.では ma=-kx を解くのに，三角関数の範囲で解を探しますが，それだけでいいのでしょうか． この手法は物理学ではよくやるものだと思うのですが，自然現象がとりうる解の集合をすでに限定してしまっていて，そのなかで妥当そうな特解を得てきて，これが得たい解だと言い張ることに意味があるのか疑問です．

抽象的な話で申し訳ないですが，よろしくお願いいたします．

やかん さんのレス (2006/04/14(Fri) 13:56)

sangaさん，はじめまして！私は理学部出身ではないので，正確な事は申し上げられないのですが，普段，私が思っている考えを書いてみます（正しい事かどうかわかりませんが）． Newton's eqは数学で言う”平行線は交わらない”のような公理と違って，実験データから作られた実験式だと思います（その昔は，力は加速度ではなくて速度に比例すると考えられていた時代もあるとか・・・）．だから，自然現象は当然ある精度で説明できる（説明できるような式を作ったのだから）ですよね．簡単な一次方程式で，実数解が一つしかなければ，方程式はもちろん成り立つし，自然界でもその解通りに事が運ぶ，と予想されるし，実験してみればそうである事が確認できる．二次方程式などの場合，高々正負の解が出るけど，それは数学上の話で，条件から容易に不適解を棄却できる（場合が多いと思いますが）．三次以上とか，指数関数とか，難しい方程式の場合は，解析解がなく近似解しかない事もある（かな？）．そうすると，数学上の方程式解析解はあくまで方便で，たった一つの特解であろうと，自然事象を説明できれば，物理としては充分，他の方程式解存在有無の厳密な考慮は，物理的というより，数学的な興味の範疇にはいるような気がするのですがどうでしょう？数学はあくまで手段ですから，世の中の説明がつけばそれでいいような気がするのですが・・．Newton's eq自体，近似式ですし・・・．

sanga さんのレス (2006/04/14(Fri) 14:30)

早々の返信，ありがとうございます．

やかんさんの仰ることは，物理学の発展を考えれば，非常に妥当な説明だと思います．つまり，実験値の集団からある規則性を抜き出してきて，基礎方程式を作ったのだから，自然現象が基礎方程式の解になっていることはあっても，基礎方程式の他の解が自然現象に対応しているわけではないということだと思います．

ただ，いったん基礎方程式を（近似的な式であるとは思いますが）公理にすえたとき，自然科学としては，その公理を使って新たな現象の「予測」をしなければならないし，また実際そうしてきたと思うのです．そのとき，今回書かせて頂いたような方法(どんな手段にしろ解が得られればそれでよいという立場)で解を得ると，当たり前ですが，探索した解集合にそもそも自然現象に対応する解がないことが考えられます．実際の物理学者は，一般解を素直に求めて，その中から妥当な特解を探しているのでしょうか．あるいは，テキストによくあるような，妥当そうな解集合のもとでの特解を探すのに専念しているのでしょうか．もし後者だとすれば，それは自然現象を予測するという上で大きな障害となるはずです．

また，一般解が得られたとして，その中から妥当な特解を探すのも困難な仕事であるように思います．先に知られている条件を付加することで，解がひとつに絞られればいいのですが，そうでない場合は，これまた自然現象の予測という意味では問題になると思います．答えが分かっていればいいのですが…．

やかん さんのレス (2006/04/14(Fri) 15:22)

う〜ん，難しい・・・．ここから先は耳学問で，本質的に理解してるわけではないので，やかんの生意気な言い分になるのですが・・．アインシュタインの重力方程式は立式したのはアインシュタインですが，解析解の一つを発見したのは，天文台に勤めるシュバルツシルトという人だそうです（たしか）．その解によると，ブラックホールのような大きな重力場に近づくと，その中心に至る前に”この世の地平線”に達する？（書いてて意味がよくわかってません）とか言いますが，実際ブラックホールに近づいた事ないし，多分，その存在の傍証となるデータすらもないのでは？実験装置もないし・・・．これは例えの一つとしてあげたつもりなのですが，求めた解析解を実験，実測で確かめられればよし，確かめられない以上パズルの解法と同じで，いずれの解も，それぞれの学者の仮説のよりどころとして，フワフワと残るのではないでしょうか？（実験，実測で正否が証明されるまで）

sanga さんのレス (2006/04/14(Fri) 15:48)

急な質問であったのに，つきあっていただいて，本当に感謝しています． ありがとうございます．

やはり，実測されてはじめて(答えありきで)，特解を決めざるを得ないことがあるということなのですね．どうしても，公理というと絶対的なものというイメージを持ってしまうのですが，数学ではないので，基礎方程式の他に束縛条件を付け加えて，特解を選別したり，実測を待ったりする必要があるということですね．

基礎方程式は「自然現象の必要条件」を取りだしたものということでしょうか．

やかん さんのレス (2006/04/14(Fri) 17:13)

「自然現象の必要条件」である！と，人間が思って（信じて）取り出したものかもしれませんね．自然が数学的にできてるんじゃなくて，自然を数学的になんとか解釈しようと努力する，極端な話，物理現象解釈の必要に迫られて新しい数学が開発されたりもする，のでしょうかね・・・．

山本明 さんのレス (2006/04/14(Fri) 22:57)

sangaさん，はじめまして． 議論を流し読みしただけなので，的を外した返答になってしまうかもしれませんが，お許しください．

>またこれに絡んだ話ですが，Newton's eq.では >ma=-kx >を解くのに，三角関数の範囲で解を探しますが，それだけでいいのでしょうか．

これについては，微分方程式の解の一意性が関係しています．解の一意性とは，ある初期条件(上の例で言うと，ある時刻での位置と速度)があればその条件を満たす解は1つだけ(=複数は存在しない)という微分方程式の(数学で証明済みの)性質です．

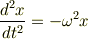
という微分方程式に対して，

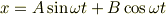
という形(A,Bが不定定数)で解を探しても，

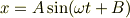
でも

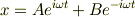
でも，同じ初期条件さえ課せば，同じ解(同じ運動)を示すことになります．

「この世界には物体の動きを規定する基礎方程式がある」というのは，物理学における信念です． そして仮にその基礎方程式に「ある時刻での運動が決っていたらその後の運動は一意に決まる」という性質があるとしましょう．とすると，“なにはともあれ，ある状況を説明できそうな解っぽいものを見付けられたら，その解っぽいものは本当の解(現実を説明する解)と，さほど違わないはず”だ…という発想に繋がるわけです．

ちなみに基礎方程式として，Newton方程式ならば解の一意性は数学的にちゃんと証明されているので，それを基礎方程式であると信じる限りにおいて，上の発想はあながち悪くないと思います． だけど新しく理論体系を考えていくと，できたての“基礎方程式”は必ずしも解の一意性が証明されているわけではありません．けれど，そんなときでも「正しい基礎方程式ならば，解の一意性は(たとえ難しくても)きっと証明できるはず」というスタンスで，一意性の証明が試みられたりします．だって現実社会での現象を見てると，一意性がありそうだから…という単純な期待，というか信念です．

…といったところで，質問への返答になってますか??

sanga さんのレス (2006/04/15(Sat) 12:52)

私の質問したかった内容そのもののご返答でした．ありがとうございます．

現実の一意性と式から得られる解の一意性をからめた議論は，化学でもよくするのですが，物理学も同様の哲学に基づいていたのですね．

確かに，（現実が一意に決まる範囲で）基礎方程式とその他の条件を満たす解が「一意」に決まるならば，それを公理系とすることで，どんな求め方をしてもいいことになりますね．

何から何までお聞きして申し訳ないのですが，こういった内容まで踏み込んで書いた物理学の書籍というものはありますでしょうか．物理学は確かに綺麗な体系ですが，その哲学をくみとれば，より深く式変形の理由などが理解できるようになる気がします．

山旅人 さんのレス (2006/04/15(Sat) 13:52)

sanga さん，初めまして．山旅人と申す老爺です． お求めに叶うかどうかですが，以上を読ませていただく限りでは， 『力学』（ランダウ・リフシッツ理論物理学教程） http://www.negitaku.org/item.php?p=4489011601 が最も近いと思います．ですが，初学者には難解です． 日本人の本では，『現代物理学を学ぶための古典力学』（伏見康治・著 岩波）ですが，残念ながら絶版で手に入りません．神保町で捜す価値はあり．大きな図書館にならあるでしょうから，気が向かれたらどうぞ．

sanga さんのレス (2006/04/15(Sat) 16:48)

ランダウはやはり有名ですが，そんな方向まで書いているとは思いませんでした． ランダウの教程は，力学というよりも，ほぼ解析力学ですので，まだまだ準備が不足な状態です．後者を一度読んでみようと思います．

本当に沢山の返信，ありがとうございました． この掲示板に書き込んでよかったです．今後とも，よろしくお願いいたします．