飲みすぎ さんの書込 (2006/03/31(Fri) 20:00)

テニス好きの会社員ですが， 単純なことの筈なのになかなか解けない疑問を払拭したく， こちらに書き込みすることに致しました．

以下に内容を記述しますが，もし間違っていたら是非ご指摘願いたく， どうかどうか宜しくお願い致します．m(__)m

−−− 止まったボールを叩いてＶの速度になる現象を運動量の式で表すと， ｍ・Ｖ＝Ｆ・Δｔ＝ｍ・ａ・Δｔ つまり，ボールはある加速度でその速度まで到達しているということですが， ここで以下の疑問が出ました．

<<<疑問の内容>>>

●テニスプロの方々のラケットのスイングスピードを単純に見積もると・・・ （ラケットで，２ｍの距離を等加速度で０．２秒でスイングすると考えて （見積もった場合なら，スイングスピードは72km/h(20m/s)程． （つまり，それ以上のスピードになると，ボールに加速を加えられない （様に感じてしまっています．．

●ただ，実際にプロがラケットでボールを打つと・・・ サーブは240km/h(67m/s)程度， ストロークは100km/h(28m/s)以上は出る最近です．

●とすると，20m/s以上のスピードを稼ぎ出して67m/sものスピードに到達しているのは， 「ボールを打つときのボール自身の反発スピード＋ラケットの反発スピード」ということ なのだろうか？（つまり，それら無しでは，サーブ240km/h，ストローク100km/hは 有り得ないのだろうか？）

●ただ，よくよく考えてみると野球などでは，硬球の反発スピードはあまり期待できないのに 平気でピッチャーが100km/h以上のボールを投げています．これも不思議．．

・・・・という疑問です． どうかどうかご感想・ご指摘をいただきたく，宜しくお願い致します．m(__)m

Joh さんのレス (2006/03/31(Fri) 21:10)

よくわかりませんが，右辺のm・a・△tのmは，ボールの質量じゃなくて，ラケット（+腕？）の質量なんじゃないでしょうか？

飲みすぎ さんのレス (2006/04/01(Sat) 14:21)

＞＞Joh様

ご回答ただき，ありがとうございます．（分かり辛い質問で本当に申し訳ありません．．）

>右辺のm・a・△tのmは，ボールの質量じゃなくて，ラケット（+腕？）の質量なんじゃないでしょうか？

なるほど，右辺のＦはラケット（+腕？）側の物だからということですね． （間違っていたらご指摘ください．．）

たけだ さんのレス (2006/04/01(Sat) 20:13)

飲みすぎさんこんばんは． 面白い問題提起ですね．

この問題は，単純化すると止まっている球に重たい球をぶつけた場合，ぶつけられた球の速度はどこまであがるか？ と同じ問題と考えます．

そこで，計算を始めたのですが，この様な問題では，ネットの方が早いと思い調べてみました． その結果，次のような物が見つかりました．

• http://sci-tech.ksc.kwansei.ac.jp/d_phys/education/demo_physics/demo_mech1.pdf#search= '

これで見ますと，ぶつけた球の速度の2倍まではぶつけられた球の速度は上がるようですね． これは，私にとっても意外な結果でした．

やかん さんのレス (2006/04/03(Mon) 16:43)

たけださん，こんにちは！ 小さくて静止している球の質量を 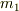，衝突後の速度を 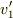， 大きい球の質量を 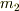，衝突前速度を 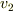，衝突後速度を 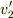とすると，運動量保存より 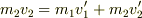運動エネルギー保存より

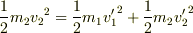
これより 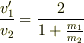あっ，本当だー！ ・・・(゜O゜;) 知らんかった〜 (^^;

ところで，飲みすぎさんのご質問なのですが，ラケットや，硬球を投げる手は等速運動をしてるわけではなくて，加速してますよね．つまり，力がかかっている．ボールに触れている時間だけ，力積を受けるわけで，それで運動量が変化するから，等速運動の玉や，ラケットが衝突した運動量交換時よりも，スピードが出ていいのではないでしょうか？ 言ってる事間違っていたらすみません・・・． (^^;

Dr.Strange Lab さんのレス (2006/04/03(Mon) 21:36)

やかんさん>ボールに触れている時間だけ，力積を受けるわけで， 運動量の交換にはボール同士が触れている時間は関係無さそうに思えますが…

飲みすぎさん>サーブは240km/h(67m/s)程度， 飲みすぎさん>ストロークは100km/h(28m/s)以上は出る最近です． 飲みすぎさん>野球などでは（略）100km/h以上のボールを投げています．

これは腕のしなりを使っているのではないかと． 肩の筋肉＋前方への踏み込みが作り出した体全体の運動量を腕の先に伝達するわけです． ちょうどムチを振って波を先端に向かわせるような感じです． 運動量が腕の先端に向かって移動するにつれ，そこから先の質量は減少しますから, 速度が増大します．最後に手首まで運動量が伝達したところで，野球ならボールを放す， テニスならラケットをがっちり握って手首の動きをラケットの長さで拡大します．

というようなプロセスだと思うのですが…計算してみないといけませんがね．

ちなみに長さ数mのムチの場合，上手くしならせれば先端は音速を超えるそうです．

たけだ さんのレス (2006/04/03(Mon) 21:46)

やかんさんこんばんは． 私が途中までやって，面倒なので止めてしまった計算をやって頂きありがとうございました．

また，最後の部分のご指摘鋭いですね． たしかに，その通りなのですが，計算するとなるとモデル作りから始める必要があり，一寸大変ですね．

この2倍になるのは，計算しなくても推測できるのがわかりました．

今，直方体の大きな物体を静止している小さな球体にｖの速度であてたとします． その場合，反発係数を１とすると，大きな物体に乗っている人から見るとｖの速度で小さな球体が飛んできて，同じｖの速度で反発したことになります．

これをモデル化すると，大きな物体と小さな球体との間に理想的なバネをいれると良さそうです． そうすると，球体が停止した状態では，小さな球体の運動のエネルギーEがバネに蓄えられます． そして，そのエネルギーEで球体が飛ばされることになります．

これが等速運動でなく，加速度がついていれば，球体が停止した段階でのバネに蓄えられるエネルギーは増えます． また，球体を飛ばす段階でもエネルギーは増えます．

そう考えると，確かにご指摘の通りより大きなスピードになりそうですね．

飲みすぎ さんのレス (2006/04/04(Tue) 00:41)

＞＞たけだ様，やかん様

ご回答ありがとうございます．．

>これで見ますと，ぶつけた球の速度の2倍まではぶつけられた球の速度は >上がるようですね．

考えてみたのですが，この算出式は，

Ｖ2'＝Ｖ2＋ｍ1・(１＋ｅ)・(Ｖ1−Ｖ2)／(ｍ1＋ｍ2)・・・（ご提示の資料から） ↓ ↓（ｍ1をラケット(+腕)，ｍ2をボール，ｍ1＞＞ｍ2，Ｖ2＝０として・・） ↓ Ｖ2'/Ｖ1＝(１＋ｅ)／(１＋(ｍ2/ｍ1)) ↓ ↓（ｍ2/ｍ1→０，０≦ｅ≦１とすると・・） ↓ １≦Ｖ2'/Ｖ1≦２

・・ということと自分は解釈しました． （衝撃にエネルギー保存則を使うのに違和感があって・・．） （もし間違っていましたらご指摘ください．．） 実際の物の動きをイメージする事は未だできませんが， きっとそのような動きになるのでしょうね．． これを手掛かりにイメージを広げていこうと思っております． ありがとうございました．

>ボールに触れている時間だけ，力積を受けるわけで，それで運動量が変化するから， >等速運動の玉や，ラケットが衝突した運動量交換時よりも，スピードが出ていいの >ではないでしょうか？

いわゆる「フォロースルーを大きく取る程，速度が増す」と言うこと なのかもしれませんね．（ゴルフ話でその様な話を聞いたことがあります．） 少しでも力を掛ければ速度は上がる・・・ただ，自分の動作速度以上の速度に なったものに力を加える場合はやはり工夫がいる気がしてきました． （目指す先は長そうです．．）

飲みすぎ さんのレス (2006/04/04(Tue) 00:53)

＞＞皆様

ご指摘が増えているのを見逃してしまい，申し訳ありません．． 色々とありがとうございます．よく読んで参考にさせていただきます．．

やかん さんのレス (2006/04/04(Tue) 15:44)

Dr.Strange Labさん，こんにちは！

＞運動量の交換にはボール同士が触れている時間は関係無さそうに思えますが…

う〜ん，やっぱ私間違えたかなあ・・・． (^^;

＞飲みすぎさん この式でも同じように良い気がします．

＞たけださん

＞これをモデル化すると，大きな物体と小さな球体との間に理想的なバネをいれると良さそうです． そうすると，球体が停止した状態では，小さな球体の運動のエネルギーEがバネに蓄えられます． そして，そのエネルギーEで球体が飛ばされることになります． これが等速運動でなく，加速度がついていれば，球体が停止した段階でのバネに蓄えられるエネルギーは増えます． また，球体を飛ばす段階でもエネルギーは増えます．

あっ，これわかりやすい！完全弾性衝突って，要するに理想的なバネが入っている状態，物体自体が，ひしゃげたままにならず，原型に復元する理想バネみたいな事なんですね．だから接触している間，更に加速すると，運動量，エネルギーとも増える・・・．

Dr.Strange Lab さんのレス (2006/04/04(Tue) 22:35)

私＞運動量の交換にはボール同士が触れている時間は関係無さそうに思えますが… やかんさん＞う〜ん，やっぱ私間違えたかなあ・・・．

物体a,bの質量及び速度をMa，Mb及び速度をVa，Vbとし， 接触中にお互いに及ぼす力をFとすると，作用反作用の法則から， Ma(dVa/dt)= F…(1) Mb(dVb/dt)=-F…(2)

(1)+(2)＝Ma(dVa/dt) + Mb(dVb/dt) = 0 これを積分して MaVa + MbVb = const が運動量保存ですから，接触時間は式に現れないということじゃないかと．

たけださん＞これをモデル化すると，大きな物体と小さな球体との間に たけださん＞理想的なバネをいれると良さそうです． たけださん＞球体が停止した状態では，小さな球体の運動のエネルギーEが たけださん＞バネに蓄えられます． たけださん＞そして，そのエネルギーEで球体が飛ばされることになります．

この場合バネを縮めた力をFとすると，バネの反対側に同じ力Fが働きますから， 上の式と同じになるので普通の運動量保存と同じになると思います．

たけださん＞これが等速運動でなく，加速度がついていれば，球体が停止した段階での たけださん＞バネに蓄えられるエネルギーは増えます．

バネの左端に物体aが当たった時刻から物体aに右向きの外力Fを与えるとすると， MaMb ○→|-mmmm-|o

Mb(d2Xb/dt2) = k(Xa - Xb)…(1) Ma(d2Xa/dt2) =-k(Xa - Xb) + F…(2)

X = (MbXb+MaXa)/(Ma+Mb)と置くと，(物体aとbの重心位置) (1)+(2) = (Ma d2Xa/dt2 + Mb d2Xb/dt2) = dX2/dt2 = F/(Ma+Mb)

つまり2物体の重心Xが右へ加速度F/(Ma+Mb)で加速度運動することになります． このとき，重心から見ると 物体bはFMb/(Ma+Mb)の力でバネを左へ縮め， 物体aはFMa/(Ma+Mb)の力でバネを左へ伸ばしているように見えます． するとバネの伸びは一定になり，バネに蓄えられているエネルギーは一定， 物体aとbの運動エネルギーだけが増大する…ように思えるのですが．

たけだ さんのレス (2006/04/05(Wed) 10:55)

Dr.Strange Labさん，はじめまして 数式を駆使した詳細な反論，ご苦労様でした． これだけの式をすらすら書けるとは，すばらしい能力ですね． ただ私は化学が専門で，これらに対して詳しく解析して反論するだけの能力がありまませんので，私なりの解釈でご容赦下さい．

まず，問題を整理しますと，最初に飲みすぎさんが疑問をだされたのは，ラケットの速度より，打たれた後の球の速度が大分速いように思うがなぜか？ だと思います． これに対しては，２球の衝突の理論からラケットの2倍近くの速度がでても不思議ではないと計算されました． これに対しては皆様納得されたようです．

ただ，それに付加するものとして，やかんさんから，ラケットで球を打つ場合，球にラケットが触れた瞬間に力を抜いてしまう（等速度での衝突）より，ずっと力を入れ続けた方が，より球の速度がよりあがるのでは？と指摘がありました． それで，私なりのモデルでその可能性があることを示したつもりです． （これに関しては，ｂの運動エネルギーが増加するとされているのでDr.Strange Lab，さんも同意されていると考えます．）

また，その機構ですが，私なりのモデルでは 今，直方体の大きな物体を静止している小さな球体にｖの速度であてたとします． その場合，反発係数を１とすると，大きな物体に乗っている人から見るとｖの速度で小さな球体が飛んできて，同じｖの速度で反発したことになります．

これをモデル化するには，大きな物体と小さな球体との間に理想的なバネをいれると良さそうです． そうすると，球体が停止した状態では，小さな球体の運動のエネルギーEがバネに蓄えられます． そして，そのエネルギーEで球体が飛ばされることになります．

これが等速運動でなく，加速度がついていれば，直方体から見て，球体がバネに接触し縮んで球体が停止し，その後バネが少しずつ伸びて球体を跳ね飛ばす間，少しずつ直方体は前方に進んでいることになります． その相当分だけ，バネに蓄えられるエネルギーは加速度が無い場合に比べて増えます． そして，球はより早く飛び出すと考えられます．

以上が私の考え方ですが，Dr.Strange Labさんの >バネの伸びは一定になり，バネに蓄えられているエネルギーは一定 との部分が私には理解できませんでした．

あと少し補足ですが， 私＞運動量の交換にはボール同士が触れている時間は関係無さそうに思えますが… やかんさん＞う〜ん，やっぱ私間違えたかなあ・・・． の部分は，ラケットに加速度が付いている場合を考えていると思われるので，普通の衝突の式は使えないのでは？

やかんさんの ＞飲みすぎさん この式でも同じように良い気がします． の部分ですが，私も同じように計算を始めたので，第一近似としては正解です． ただ，ホームページの式では，eが１でない場合も考えているので，より範囲が広いと考えられます．

飲みすぎさんの ・・ということと自分は解釈しました． はそれで良いと思います．

また 実際の物の動きをイメージする事は未だできませんが， きっとそのような動きになるのでしょうね．． の部分は直方体を使った上記のモデルを考えるとより分かり易いのではないでしょうか．

間違っている部分もありそうですが，専門外なのでご勘弁下さい．

やかん さんのレス (2006/04/05(Wed) 13:13)

うう，難しいなあ・・・． Dr.Strange Labさんの書かれた式はもちろん正しいし・・・． バットで硬球を打つような場合，バットから運動量をもらうんじゃなくて バットから力を接触時間の分だけ力積として受け，硬球の運動量が変化する， ような気がするのですが・・・．

Joh さんのレス (2006/04/05(Wed) 20:10)

バネが出てきたあたりから，私はもう話についていけないのですが， 私もやかんさんと同じような感想です．

ボールはつぶれるので，接触時間が零ではなく，この間にバットなり ラケットから受けた力で加速するって考えたらいけないんでしょうか？

Dr.Strange Lab さんのレス (2006/04/05(Wed) 20:36)

長々とすみません．これで終わりです． 少々勘違いがありました． たけださんの大きな物体を物体a，小さな球体を物体bとして， 質量をM,位置をX,バネ定数をkとします．（それぞれに添字aまたはbをつける） バネの自然長loを入れて Mb(d2Xb/dt2) = k(Xa - Xb - lo)…(1) Ma(d2Xa/dt2) =-k(Xa - Xb - lo) + F…(2) のようにして解きます． 途中を省略すると，物体aと物体bは加速度F/(Ma+Mb)で運動する両者の重心から見て， 単振動する形になります．

勘違いというのは，物体bがバネにくっついたまま，物体aともども加速される と考えてしまった点です．この場合，単振動でバネが伸び縮みしながら 全体の重心が力Fにより加速していきます． 単振動の振幅（=Fで決まるバネの縮み量）は衝突時に決まってしまうため， いくら力Fを与えている時間を長くしても，バネに蓄えられる エネルギーは一定です，というのが前に書いた結論です．

実際は物体bはバネに固定しているわけではないので，単振動を開始して 半周期後には物体bはバネから離れることになります． 上の(1)，(2)を解くと，単振動の周期Tが T＝2π/ω＝2π/√{k(Ma+Mb)/(MaMb)}で決まるので， バネとの接触時間は物体aに加える力Fによらないとの結果になります． しかし，物体bが半周期後にバネから離れるときの速度にもFが入ってくる （振幅にFが含まれるので，微分して得た物体bの速度にもFが含まれる）ため, 力Fによる加速は存在することになります．

バットとボールの接触時間は数ms（らしい）であり，これを5msとすると， その間に50kgfの力を受けたとして，ボールを0.15kg，バットを0.75kgとして その速度増加は50×9.8/(0.15+0.75)×0.005=2.7m/s=9.8km/h なので，ちょっと加速が小さいような気もしますが…

たけだ さんのレス (2006/04/05(Wed) 22:46)

やかんさん，Johさん， Dr.Strange Labさん レスをありがとうございました．

>バットから力を接触時間の分だけ力積として受け，硬球の運動量が変化する， >ような気がするのですが・・・． その解釈で良いとおもいますよ．

>ボールはつぶれるので，接触時間が零ではなく，この間にバットなり >ラケットから受けた力で加速するって考えたらいけないんでしょうか？ 確かにその通りですが，それを数式化して定量的に計算できる一手段としてバネを採用したにすぎません．

>少々勘違いがありました． 了解しました． しかし，単振動がでてくるとは思いませんでした．

皆様の投稿を見てみると，一つの問題でも人によって実に色々の考え方があるのが分かり非常に有益でした． これで，各人の職業などのバックグラウンドも分かるともっと面白いでしょうね．

私もこの問題でこんなに深入りするつもりはなかったのですが，随分長くなってしまいました． これで，終わりにしたいと思います． どうもありがとうございました．

飲みすぎ さんのレス (2006/04/06(Thu) 05:41)

＞＞皆様

色々なご意見，本当にありがとうございます．

実はこの疑問は，元テニスプロの方を交えて意見交換されているところで 出てきている疑問だったりします．ラケットとボールとのインパクトについての 明確化，合理化が目指すところですが，参考になりそうな書籍類が意外と見付からず， 困っていたところです．

皆様のご意見を大いに参考にさせていただこうと思っております． ありがとうございました．m(__)m