運動量と運動のエネルギーの保存について

この辺につきましては，「ネーターの定理」というものが知られており，保存則と対称性について，綿密な考察がされておりますので，参考になれば幸いです．＃丁度記述されている方が居られました．＃ http://homepage3.nifty.com/iromono/PhysTips/conserve.html ＃興味が御座いましたら，「CP非保存」について調べてもいいかもしれません．

Re: 運動量と運動のエネルギーの保存について

tomo さんのレス (2006/03/30(Thu) 13:32)

先端のスイカさん，みなさん，こんにちは． tomoです．

> 運動量が保存される条件とは何なのでしょうか．

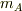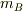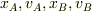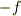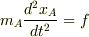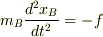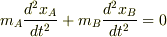スパイクさんのおっしゃる通り，運動量保存則はネーターの定理から導かれます．そこまで踏み込まなくても，簡単には以下のような説明もできます． <pre> AB ○------------●</pre> 水平面上に置かれた，ばねでつながれた物体A（質量 m_A ）と物体B（質量 m_B ）を考えます．時刻での物体Aの位置および速度，物体Bの位置および速度をそれぞれ x_A, v_A, x_B, v_B で表します．物体Aがばねから受ける力をとすると，物体Bがばねから受ける力はとなります．運動方程式を立てますと，物体A $m_A\frac{d^2x_A}{dt^2}=f$ 物体B $m_B\frac{d^2x_B}{dt^2}=-f$ 両辺を加えると $m_A\frac{d^2x_A}{dt^2}+m_B\frac{d^2x_B}{dt^2}=0$ となります．ここで，右辺がになることがポイントです．さらに計算しますと， $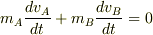m_A\frac{dv_A}{dt}+m_B\frac{dv_B}{dt}=0$ $\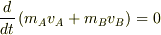frac{d}{dt}\left(m_Av_A+m_Bv_B\right)=0$ となり，運動量の総和の時間微分が，つまり，運動量の総和が時間変化しない＝保存するということになります．運動方程式を足し合わせて右辺がになるということは，その系には内力しか働いていないということを意味しています．

> 等速直線運動する貨車が坂道を登る例

においては，重力という外力が運動方程式の中に入ってきますので，運動方程式を足し合わせたときに右辺はになりません．したがって，上記のような過程を経ても，運動量の総和の時間微分がにならないため，運動量は保存しません．

ここでは，物体にかかる力の様子が分かりやすいように，ばねでつながれた2物体を例に挙げましたが，先端のスイカさんが最初に挙げられたような例でも，同様です． 3物体以上でも内力のみ働く系であれば，これも同様です．

＃不正確な表現があるかもしれません．お許しを．

Re: 運動量と運動のエネルギーの保存について

Joh さんのレス (2006/03/31(Fri) 02:37)

みなさんが説明されていることの更に繰り返しになりますが，

『運動量の変化』＝『系に加えられた力積』『運動エネルギーの変化』＝『系に加えられた仕事』

という式は，高校の物理の範囲と思います．「なぜ保存則がなりたつのか？」という問題は，なかなか深遠なものだと思いますが，保存則がなりたつ条件は，力積や仕事が零の場合だと考えたら良いのではないでしょうか？

見当違いの返事だったら，すみません m(_ _)m

[home] [掲示板] [ページの先頭]