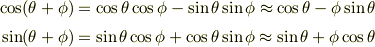いち さんの書込 (2006/03/10(Fri) 02:09)

みなさんはじめまして，僕は工学系の大学に通う彼女のいない１９歳です． 物理の問題を解いていたら解答にちょっと不明な点があったので質問させてください． 解答では

φが微小のときcos(θ＋φ)＝cosθーφsinθ，sin(θ＋φ)＝sinθ

と近似できると書かれていました．cos(θ＋φ)の方は理解できるのですが， sin(θ＋φ)はsin(θ＋φ)＝sinθ＋φcosθになるのではないでしょうか？ どうも近似の考え方が身についていないようなのでどなたか教えていただければうれしいです

やかん さんのレス (2006/03/10(Fri) 17:17)

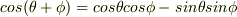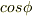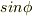いちさん，はじめまして． ですよね． がゼロに近づくと， は１に近づき， 一方， は に近づくから，だと思います．

toorisugari no Hiro さんのレス (2006/03/10(Fri) 17:38)

いちさんの考え方で正しいと思います．

やかん さんのレス (2006/03/10(Fri) 17:52)

あれっ，さっき確かに良く読んだつもりが，いちさんのご質問の問題を間違えたようですね．すみません．m(__)mtoorisugari no Hiroさんのお書きになった式通りですね． :)

toorisugari no Hiro さんのレス (2006/03/10(Fri) 17:57)

> いちさんの考え方で正しいと思います．

ただし，条件がこれだけしかないとしたらです．

もし 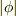も 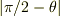も同程度に小さいのなら， 問題となった式が正しいです．

いち さんのレス (2006/03/10(Fri) 19:34)

やかんさん，toorisugari no Hiroさん，ありがとうございました どうやらπ／２ーθも微小という問題だったようです 問題文中に明記されていない条件を見つけるのは難しいです