あいちゃん さんの書込 (2006/02/15(Wed) 22:30)

はじめまして．私は病院で理学療法士（リハビリ）の仕事をしているあいちゃんと申します． 現在，病院で患者様の治療をしておりますが，どうしても原因がわからないものなどは，遠くの施設にある三次元動作解析装置と床反力計を使って計測してその原因と治療法などの参考にしております．

三次元動作解析を使っているといっても，私は根っから文系で，最近ようやくモーメント等を理解している状態です．

ここからが本題なのですが，最近出会った文献で下肢関節のモーメントを求める方法でなく，関節，もしくは下肢自体の剛性を求める方法があるとのことでした．

単純に説明すると下肢全体を1つの剛体と考えた時，足首のところでどれだけ剛性があるかという問題のようです．（外乱を加えた時の強度といってもいいのかも） そこで出てきたのが剛性楕円なのですが， 本屋さんに足を運んでもそれらしき本が無く，またインターネットではhitするものが地質工学とかかなり難解な数式で，とりあえず「これは使えないな」ということがわかるだけでした．

もし，工学系の方がいらっしゃいましたらどんな本を参考にしたらよいか教えて頂きたいのですが…． もしくは剛性の勉強をする（関節を跨いだ筋肉を考えるので弾性とした方がいいのでしょうか？）には，どんな順番で行えばよいでしょうか？

みなさまお忙しいとは思いますが，ヒントだけでも頂けたら幸いです． よろしくお願いします．

PSここに書いてある物理についての解説は凄く為になりますね．もう少し早くこのHPを見つけていたら今までの苦労をしなくてもよかったと思います．（笑）

黒子 さんのレス (2006/02/16(Thu) 23:12)

はじめまして．工学系の大学3回生の黒子と申します．

ご質問の「剛性楕円」について，自分の大学の図書館でも少しだけ剛体力学の本を調べたのですが，なかなかその単語に出会えませんでした． で，確かにインターネットでもあまり有用と思えるサイトに出会えません． 私は機械系ではないので，剛体力学もとんと昔にやった人なのですが， 「剛性楕円」について， ・楕円の形をした剛体の剛性 ・ある剛体の剛性を示したときに数学的に楕円の軌跡を描く とかなんじゃないかな・・・と予想を立ててみました．（あくまで予想です！！）

また，調べて何かはっきりしたことが分かれば，お知らせします．

Joh さんのレス (2006/02/17(Fri) 00:13)

私も詳しくありませんが，もしかして慣性楕円体のことまもしれません．

剛体の回転の運動方程式(オイラー方程式といいます)は，角速度と慣性モーメントで書かれますが，慣性モーメントは２次のテンソルなので，３×３の行列の形で表現できます．そこで一般には９つの成分があります．しかし，行列の対角化ができますので，３つの主軸方向と対角成分に表現を集約できます．主軸は直交しますので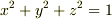， の形で慣性モーメントを表現できます．これが慣性楕円体です．慣性楕円体を使うと，どんな形の物でも，慣性モーメントの特性を楕円体で表現できるということです．

あいちゃん さんのレス (2006/02/19(Sun) 19:00)

黒子さん，JOHさん．回答ありがとうございます． 必死に大きな本屋さんの理工系の棚を探すこと３時間，ありました． ロボット工学で使うみたいです． いきなり難しいものは読めないので，とりあえず「はじめてのロボット工学」を 買って帰りました． ロボットって凄く遠い存在のようでしたが，この本を読むと日常生活のいたるところに存在するんですね．いやー，目からうろこでした．

オイラー方程式は気合で勉強してみますね． ところで，楕円や円って不思議なものですね．楕円についても勉強してみます．

たけだ さんのレス (2006/02/27(Mon) 14:12)

あいちゃんさん，今晩は．

剛体の力学，ことに回転に関することをベクトルで考えるのはとても頭の痛いことと思います． オイラー方程式なども理解しようとすると専門家以外の人にはかなりの抵抗がありそうです．

私は，コマに興味があり，ホームページを作ってみましたが，非常に分かり易いので，一度見ていただければ幸いです．

ベクトル表現の意味がよく分かりますので，多分，これからの勉強の助けになるのではと自負しております． では，また

（昨日投稿したのですが消えてしまいました．内容的に問題があるのでしたらご指摘頂ければありがたく，宜しくお願いいたします．） たけだ

山本明 さんのレス (2006/02/27(Mon) 15:40)

＞たけだ さま

はじめまして．掲示板の監視係の一人の山本です．

実は今朝方，システムの不調で最近の書き込みの一部が消えてしまいました．決して，書き込みに問題があったわけではありません．ご迷惑をおかけしました． たけださまにはご不快な思いを抱かれたかもしれませんが，どうぞお許しください．

＃地球ごま，私も持ってますけど，面白いですよね．

たけだ さんのレス (2006/02/28(Tue) 09:47)

山本様 はじめまして． 掲示板の監視役もされているとのこと，ご苦労様です．

コマの原理については，いわゆるトンデモものがあり，同じ仲間と思われて削除されてしまったのでは？ と心配しましたが，システム不調が原因と分かり安心しました． 色々お気遣いありがとうございました．

ここのホームページ，掲示板は程度が高く，いつも楽しく勉強させて頂いております． 益々のご発展を期待しております．

あいちゃん さんのレス (2006/03/02(Thu) 21:48)

たけだ様，こんばんは． さっそくHPにこれからお邪魔させて頂きます．

剛性にしろ，物体の回転にしろ，何故楕円で表せるのでしょうか？ そのなぞが解けるのでしょうか？ 今も「ロボット工学の運動学」という本を読んでいますが 理解不能な領域に入ってしまってます． でも，ここからやれば出来るよ！という道って無いんでしょうね． 興味のあるところから１つずつ，一個一個理解しながら理解していけば いいんでしょうけど・・・．やっぱりわからない． このHPにあるように，図形でこんなことだよってイメージがつかめればいいんでしょうが・・・．

でも，こういったHPって貴重ですよね．感謝しております．

PS 今日はラプラス変換に手こずってます．

トンガリ さんのレス (2006/04/21(Fri) 10:35)

剛性と言えば材料力学です．【剛性楕円】は，きっと材料力学の用語でしょう．

最新材料力学（大久保肇著 朝倉書店刊 1957年初版 1973年26版）の『非対称荷重を受ける梁の撓み』 の中で ・・・ただし，『非対称荷重』は適切な表現でなく『断面の図心を通り主軸と角度をなす荷重』の意味

Ａ ：断面の面積 ｘ，ｙ ：断面の主軸 Ｉｘ，Ｉｙ ：主軸ｘ，ｙに関する《慣性モーメント》 とすると，

楕円 ｙ＾２／Ｉｘ ＋ ｘ＾２／Ｉｙ ＝ １／Ａ をその断面の《慣性楕円》 という．

とあります．材料力学を学ぶ者にとって， 用語《慣性モーメント》は正しくは ＜断面二次モーメント＞ であると解釈するのが常識です． ＜断面二次モーメント＞ は 【剛性】を評価するための重要な尺度の一つです．

機械工学では，凧糸巻きのＩ字型平板は《慣性モーメント》で慣性力を評価し， 鉄道レールのＩ字型断面は ＜断面二次モーメント＞ で剛性を評価します．しかし，両者は酷似しています． 凧糸巻きのＩ字型平板の質量分布の中心を重心，鉄道レールのＩ字型断面の面積分布の中心を図心と呼びます． 材料力学で剛体の力学に似た様な式や概念は，歴史的に先に発達した剛体の力学の用語を誤用しがちです．

歴史が古い学問なので，用語が著者によって異なり，下記の三つの用語は同一物を表すと考えられます． 《慣性楕円》 → ＜断面二次モーメントの楕円＞ → 【剛性楕円】

用語で権威あるのは，私の手元にありませんが，日本機械学会の『機械工学便覧』の『材料力学』でしょう． この書物を読まれると問題が解決することでしょう．

ところで，この問題の発端は， 人間の下肢の前後方向の剛性と左右方向の剛性の実測値から，たとえば斜前30度方向の剛性を算出せよ． だったのか知らん．