えり さんの書込 (2006/02/04(Sat) 19:29)

こんばんは．今年受験の高3です．

ある問題を解いているときにつまづいてしまったのですが・・・

例えばある物体Gの速さが{Ｍv(A)+mv(b)}/Ｍ+mと表せるとします(ただし，Ｍ，v(A)は物体Aの質量と速さ，m,v(b)は物体Bの質量と速さ)．その時の物体Aのx座標をx(A)，物体Bのx座標をx(a)+Rとすると，Gの速さを[Ｍx(A)+m{x(a)+R}]/Ｍ+mと表せるのはどうしてですか？

解説では，普通に変形されていたのでよくわかりませんでした．速さは，位置で書き換えることができるのでしょうか？説明がわかりにくいかもしれませんが，教えて下さい．宜しくお願いいたします．

山本明 さんのレス (2006/02/04(Sat) 20:21)

えりさん，こんばんは．

速度と位置は全く違うものだから，単純に速さを位置で置き替えることはできませんね． 解説になにか書かれていたなら，該当する場所を全て書いてみてくれませんか？なにかわかるかもしれません．

それと「速さが{Ｍv(A)+mv(b)}/Ｍ+m」というのも，ちょっと変な気がします． 写し間違いがあるかもしれませんよ．

えり さんのレス (2006/02/04(Sat) 21:12)

わかりました．では，問題を全て書かさせていただきます． この問題には図があるのですが，ここでは描けないので，文だけで失礼します．

なめらかな床の上に，半径Rの円筒状の凹曲面POQをもつ質量Ｍの台Aがある．Aは，その右側にある壁と，水平に張られた糸によりつながれている．面PQRはなめらかで，円筒の1/2の部分からなり，その最下点O,左側をP,右側をQ,円筒面の中心をCとする．C，P，Qは同一水平線上にある．この台の左側Pより鉛直上方に距離Rだけ離れた位置から，質量Bの小球を自由落下させたところ，Bは点Pを通過後，円筒面に沿って，円運動し始めた．その後，Bが，∠PCB=30°となる位置を初めて通過した直後，糸が切れた．糸が切れた瞬間を時刻t=0とする．糸が切れた後もBは円筒面から離れることなく運動するが，このとき台Aも動く．その後，Bは，時刻t(1)の瞬間に台Aの右端Qを通過し，上方に飛び出した．ただしこの間，A,Bからなる系の重心の速度の水平成分は一定である．この一連の運動中，A,Bが壁に衝突することはないものとし，糸が切れた瞬間の台Aの最下点Oの位置を原点とする右向き正のx軸をとる．A,Bの速度の水平成分は+x向きを正とする．また，Aの重心は点Oであるとし，Aの位置は点Oの座標で表すものとする．重力加速度の大きさをgとし,以下で考える運動は，常に図の鉛直面内で起こるものとして，次の設問に答えよ．

というのが導入であり，私が躓いてしまったのは

BがAの右端Qに達した瞬間の台A(点O)のx座標を，Ｍ,m,g,R,t(1)を用いて表せ．

という問いです．そしてやはり，重心の速度の水平成分は{Ｍv(A)+mv(b)}/Ｍ+mであり，v(A),v(b)はA,Bの速度の水平成分です．

長くなって申し訳ありません・・・

tomo さんのレス (2006/02/05(Sun) 00:21)

えりさん，こんばんは． tomoです．

No.8422の書き込みの中で「重心」という言葉が何度か出てきていますが， 台Aの重心と，AとBからなる系全体の重心が，頭の中でごちゃまぜになっていませんか？

小問も含めてすべて書き，前の小問まで解答できたのなら， それをここに書いた方が，レスがつきやすいと思います．

＃ 質問を書く際のタイトルは「教えて下さい」のようなものではなく， ＃ 問題の内容をまとめた言葉にするようにしましょう．

山本明 さんのレス (2006/02/05(Sun) 03:26)

>そしてやはり，重心の速度の水平成分は{Ｍv(A)+mv(b)}/Ｍ+mであり，v(A),v(b)はA,Bの速度の水平成分です．

ここは私の勘違いでした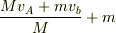． に見えたもので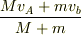． ということですね．失礼しました．

そんで最初の質問に関しては，該当の解説を書いてもらわないと，なんとも言えないのですが… ひとまず重心の位置は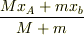， のように表わすことができますよ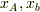．( はAの位置とbの位置)「位置」ならば． 「速さ」をそのように書くことはできません．その辺りに注意して，もう一度，解説を読んでみてはどうでしょうか??

えり さんのレス (2006/02/05(Sun) 14:25)

実は，解説にも何のコメントもなく普通に{Ｍv(A)+mv(b)}/Ｍ+m=[Ｍx(A)+m{x(a)+R}]/Ｍ+mと変形されているので，私も問題しか書く術がなくて困っているのです・・・涙．

上の式だと「重心の位置=重心の速さ」になってしまいますよね．．．私も速さ=位置の書き換えは疑問でした．もう一度よく読みこんでみます．