ベクトルポテンシャルが存在すること
ベクトルポテンシャルが存在すること
ゆかり さんの書込 (2006/01/27(Fri) 23:57)
divB↑=0⇔B↑=rotA↑を示したいのですが, 右から左はすぐに示せたのですが, 左から右が示せません. どうすればいいのか教えてください.
Re: ベクトルポテンシャルが存在すること
トミー さんのレス (2006/01/29(Sun) 22:42)
ゆかりさん,はじめまして.トミーといいます.
これは大学の先生かどなたかが出された問題なのでしょうか? 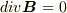 の関係が成立する時,任意のベクトル関数
の関係が成立する時,任意のベクトル関数 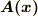 を用いて
を用いて 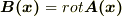 と表すことができる,というものなので,ある意味質問の左から右は自明だと思うのですが….
と表すことができる,というものなので,ある意味質問の左から右は自明だと思うのですが….
詳しくレポート等に書かなければならないようでしたら,磁場に関するガウスの法則の辺りから,ベクトルポテンシャルについてまでを勉強されると良いと思います :)
Re: ベクトルポテンシャルが存在すること
山本明 さんのレス (2006/01/30(Mon) 01:34)
あまり自明という気はしないですね,私は…. いますぐ,パッと証明はできないけど,No.7774
のときみたいに,証明できるんでしょうねぇ….どうやるんだろう・・・.
外微分を使うのは反則かな…それでもすぐにやり方は思いつかないけど・・・.
Re: ベクトルポテンシャルが存在すること
トミー さんのレス (2006/01/30(Mon) 02:53)
山本さん,ご無沙汰しております.
No.7774に対するやかんさんの返信No.7823を読んで納得がいきました.こういう証明をする必要があるのですね.
私も現段階ではどうやって証明するのかわかりません.No.7823でやかんさんが挙げておられる本に書いてあるかもしれませんね.
Re: ベクトルポテンシャルが存在すること
やかん さんのレス (2006/01/30(Mon) 17:52)
ゆかりさん,はじめまして! トミーさん,山本さん,こんにちは! 今,こないだの本を見たのですが残念ながら載ってないような・・・. そのかわり,yahooで,”ベクトルポテンシャル”,”存在”,”証明”をキーワードに調べてみたら,以下のページがありました.これで証明になりますでしょうか? (今回こそ,全く内容理解しないまま丸引用しちゃいました (^^;)
Re: ベクトルポテンシャルが存在すること
トミー さんのレス (2006/01/30(Mon) 18:41)
やかんさん,こんにちは!
参考ページを探してくださり,ありがとうございます :) 恐らくこれが,今回の解答となるのでしょうね.というのも,私は読んでいて,「ふ〜ん,そういうものなのか」としか思えなかったんです… (^^;
これは「知っていないとできない証明の技術」みたいな印象を受けました.難しいですね….電磁波工学などで当たり前のように使っていた式について,ここまで深く考えたことがなかったので,とても勉強になりました :)
Re: ベクトルポテンシャルが存在すること
toorisugari no Hiro さんのレス (2006/01/31(Tue) 13:20)
直接の証明ではないですが,フーリエ変換を既知とすれば問題は0ベクトルでない 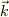 に対して
に対して
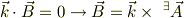
が成り立つことをを示せとなります. これを証明してみれば,「何となく」微分の場合でもイメージ出来…ないか.ま,微分を含まないベクトルの場合でも自明でないので証明してみます.
ベクトル三重積より
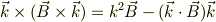
が成り立ちます.題意より 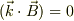 だから
だから
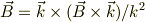
より
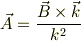
とすれば題意は満足する.
だけど,
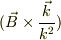 のフーリエ逆変換って…
よくわかりませんねえ.
のフーリエ逆変換って…
よくわかりませんねえ.
Re: ベクトルポテンシャルが存在すること
やかん さんのレス (2006/02/01(Wed) 15:03)
>私は読んでいて,「ふ〜ん,そういうものなのか」としか思えなかったんです…
これは「知っていないとできない証明の技術」みたいな印象を受けました.
あっ,こういう風に感じること,時々あります.特に私は人より多いような・・・ (^^; でもいろいろ証明した先人って,やっぱすごいですよねー. :)
toorisugari no Hiroさん,こんにちは!こっ,これはスマートな解法!すごい!
Re: ベクトルポテンシャルが存在すること
toorisugari no Hiro さんのレス (2006/02/03(Fri) 18:28)
> これは「知っていないとできない証明の技術」みたいな印象を受けました.
これはもっともな印象です. http://homepage1.nifty.com/th3/rot_grad_div.htm には発見法的な論理があります.しかし,そもそも, 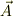 をもとめるには本来天下りな部分が絶対必要です.
をもとめるには本来天下りな部分が絶対必要です.
それは
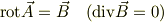
の解はこのままでは決まらないからです.
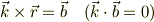
をみたす 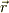 は点でなく直線
は点でなく直線
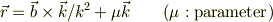
であり, 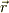 の「位置」をもとめるには不定のパラメータ
の「位置」をもとめるには不定のパラメータ 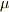 を固定しなければいけません.そのためには別の条件(たとえば
を固定しなければいけません.そのためには別の条件(たとえば 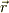 は
は 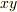 平面上(
平面上( 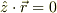 )とか
)とか 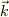 に垂直(
に垂直( 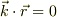 )とか)を与えてあげないといけません.
)とか)を与えてあげないといけません.
同じように微分方程式でも, 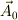 が解なら
が解なら
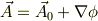
となる 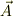 も解,という不定性があるので,何か条件をいれて関数
も解,という不定性があるので,何か条件をいれて関数  を固定しなければいけません.
を固定しなければいけません.
固定条件にはいろいろありますが,たとえば適当な基準点 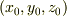 を決めて,
を決めて,
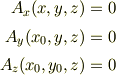
とすれば線積分で 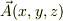 をもとめることができます.(この条件をどう決めたかの説明とか,こうなるような
をもとめることができます.(この条件をどう決めたかの説明とか,こうなるような  が存在する事の証明ははぶきます.)
が存在する事の証明ははぶきます.)
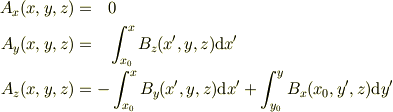
となるのを確かめてみてください.(導出もはぶきます.)
固定条件はいろいろあるので,暗黙に選んで使うと『「知っていないとできない証明の技術」みたいな印象』を与えてしまうのは仕方ないですね.
Re: ベクトルポテンシャルが存在すること
トミー さんのレス (2006/02/04(Sat) 01:50)
toorisugari no Hiroさん,はじめまして!
たくさんの証明の説明を書いてくださり,ありがとうございます :)
この証明は,本当に難しいですね.書いてくださったことを読んでいくことしかできない,というのが正直なところです.もう少しじっくり読んでみます.何か分からないことがあったら,また質問させてください.(プロジェクトメンバーなのに… (^^; )
数学的には
Stromdorf さんのレス (2006/02/04(Sat) 15:03)
前回の rot E = 0 ⇒ ∃φ : E = grad φ とか,今回の div B = 0 ⇒ ∃A : B = rot A という定理は,数学ではポアンカレの補題として知られています. 微分形式で書けば,これらは一般に dω = 0 ⇒ ∃θ : ω = dθ と表され,上の2つはこの一般的な定理の特別な場合になっています. さらに,上の例で E が有界な領域の外で 0 になっている場合は φ も有界な領域の外で 0 になっているようなものが取れる(A と B の関係についても同じ)という定理も成り立ちます. これらの証明は,数学の「微分形式」について書かれた教科書には大抵載っています.