id さんの書込 (2006/01/19(Thu) 11:04)

特殊相対論学びたての学部3年の者です． 以前こちらでお世話になったことがあります．その節はありがとうございました． 早速ですがミンコフスキー空間における（？）光の移動距離について質問させてください． そもそもミンコフスキー空間の定義を正確に知らないので語弊があるかもしれませんが・・・

世界距離（ミンコフスキー空間における距離？） は

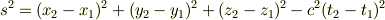
で定義されるそうですが，ここで，光源が 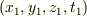にあり 生じた光の先端が 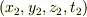にいたとすると， ミンコフスキー空間における（？）その光の移動距離について

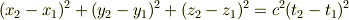
が成り立ちます．このことは即ち 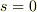であることを示していますが， 物理的に解釈して『光はミンコフスキー空間を移動しない』ということを示しているのでしょうか？

というよりも， 光速不変の原理上，上の『…』を示すようにミンコフスキー空間なるものを考えだした， ということなのでしょうか？

やかん さんのレス (2006/01/20(Fri) 19:14)

idさん，はじめまして．相対論に詳しい方のちゃんとしたレスがあるといいですね． 私は高校生並みの興味だけあるのですが，idさんのように大学でちゃんと勉強しているわけではないので，正確なこと何にも知らない，なのにレス書いちゃいかん！とも思ったのですが・・・

＞ミンコフスキー空間における（？）その光の移動距離について・・・が成り立ちます

確かに光が移動する光円錐上は移動（？）しても世界距離がゼロになりますよね．だから光はミンコフスキー空間を移動しない，と言うか，光円錐上以外へは移動しない，と言えるのかなあ．（本物の円錐想像すると，母線を這って行く距離ありそうなイメージですけど．）ミンコフスキー空間は，ローレンツ変換に対して不変なように，ミンコフスキーが数学的に解釈したもの，と昔本で読んだような気がします．このレスはもちろん回答ではなく独り言です・・・．間違ってるかもです． 認識できる世界は光速以下で，基準は光速，光速では時間の経過的な概念はゼロ？距離的な概念もゼロ？大嘘つきになりそうなのでやめます・・・． (^^;

id さんのレス (2006/01/21(Sat) 15:55)

お返事ありがとうございます． 結局『…』ということで良いんでしょうかね？ 論理として間違ってはないと思うので，そういうことにしておこうと思います．

ところで非常に素朴な質問なのですが，世界距離の定義を

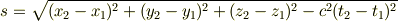
としてはいけないのでしょうか？ 読む本読む本全て 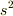で定義していますが，何か理由があるのでしょうか．

力 さんのレス (2006/01/21(Sat) 20:11)

やかんさんの勇気に敬意を表します． でも，やかんさんはちゃんと前に向かって進んでおられる，当然発言してしかるべき方です．私は座って，通り過ぎる人たちを見たりたまに声をかける程度？ ここではやかんさんのコメントがとてもこの掲示板の魅力を高めていると思います．失礼な言い方かもしれませんがやかんさんは水戸黄門で言えばうっかり八兵衛，彼がいないと水戸黄門は面白くないです（とりわけ私は，たまに出てくる博打で身を崩した甚六というところ）．

ところでＳ^2はマイナスの関係ということではないのでしょうかねー ただ単に書きやすくてかっこいいから？

やかんさんと違って私は民国府隙ーなんて今日はじめて聞きました．でもどうやったらＳ^2はマイナスになりますかね？ほんとに分かってなくてすいません．

やかん さんのレス (2006/01/21(Sat) 20:34)

力さん，こんにちは！

＞やかんさんの勇気に敬意を表します．

恐れ入ります．でも自分では勇気というよりかなりの暴挙なのでは，と・・・． うっかり八兵衛ぐらい親しまれていれば光栄なのですが．

＞結局『…』ということで良いんでしょうかね？ もともと数式上の事だから，あってる数式使うぶんには個人的なイメージ，解釈は自由だという気もしますね．世界距離がゼロのまま移動？（あー，また言っちゃった・・・．）

＞世界距離の定義を・・・としてはいけないのでしょうか？ 正負を考える手間と必要がないから？（す，すいません．）

＞でもどうやったらＳ^2はマイナスになりますかね？ 光円錐の外？（だんだん動悸がしてきました．）

そういえば特殊相対論は20数年前に大学の教養物理で習った気もするのですが もちろんとっくに忘れているし，ご質問自体はとても大切な内容で，この掲示板にふさわしい気だけはするのですが・・・． ご隠居にこれ以上迷惑かける前に風車の弥七が”とーっても危なくて見てられなかったぜー”と来ないものでしょうか？ (^^;

to さんのレス (2006/01/21(Sat) 22:21)

idさんはじめ，みなさんこんにちは．私も相対論を習い始めたところの学部２年のものです．

ミンコフスキー空間は時間と空間をごちゃ混ぜにした，四次元時空のことですよね．『光はミンコフスキー空間を移動しない』というのはおかしいという気がします．光は?s=0となるように，ミンコフスキー空間を移動していると思うのですが？やかんさんの言うとおり光円錐上を運動しているのだと思います．

s^2はローレンツ変換に対して不変です．これは三次元空間の原点からの距離の２乗が空間回転に対して不変であること似ています．しかし，四次元空間の距離?sは正だけでなく負もしくは０となることもあります．それが，光円錐に対してどのような距離をとるかに対応しているのではないでしょうか...？（自信はありませんが，はやく詳しい方の意見が聞けるといいですね☆）

かつ さんのレス (2006/01/22(Sun) 00:22)

何か，詳しい方々が遠慮されてゐるやうなので，八つァんに虐められる 悪代官の私めが，いい加減な事を書ひてみます．A(^^;)

c=1 という単位系では τ^2=t^2−s^2 として，固有時間が表されます． この時の s は三次元的な距離（座標距離）です． 慣性系自身の固有時間は自分で自分を見れば変わらないからτは 不変量である，と単純にも考えられます． （知る限りでは，海外の教科書はこんな書き方が多いような？）

で，後々，計量を考える様になると，平坦な時空（つまり特殊相対論 で表される時空）では，こういう風に定義しておけば，計量の対角成分 が 1 又は -1 になる（他の成分は０）ので，とても便利ではあります．

それが自乗で定義した理由かどうかは知りませんがｗ，別のスレッド にもありました，縦質量（相対論的質量）なんてややこしいものを導入 せずに相対論的な運動方程式を定義する事ができますわね，少なくとも．

やかん さんのレス (2006/01/22(Sun) 16:06)

toさんはじめまして．

＞やかんさんの言うとおり光円錐上を運動しているのだと思います．

えっ，あっしの思った通りで？（これ，調子に乗るな八！へ，へい・・・ (^^;）

かつさん，こんにちは！どうも危ういところを・・・（助けられた村娘）

お代官様，ここはひとつ・・，へへへ（越後屋）

idさん，レスが一杯いただけて良かったですね．原理から始まって理論的に定義された式・値でも，学習する人自身の感覚，イメージに合致させてからの方が記憶に残るし，次に他の人にも教えやすいのでは，なんて思ったりします（そういう意味で，とても良いスレなのでは，と）． わかってないのに生意気ですいません・・・．

R さんのレス (2006/01/22(Sun) 21:16)

みなさんこんにちわ． idさんのおっしゃるとおり，光速不変の原理から世界間隔を導きます． もちろん，その平方根の形で表現してもいいですが，idさんの式では本質的に虚数となります． あと，toさんの仰るとおり，三次元における回転が三角関数で表現されるのに対して，ローレンツ変換は双曲関数で表現され，x-y軸のθ回転の表式においてy→ict，θ→iψと置き換えることで形式的に得られます．

toorisugari no Hiro さんのレス (2006/01/23(Mon) 21:00)

(2次元)ミンコフスキー空間上の2点 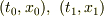の間の「距離」 は

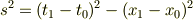
で定義されますが，この計量は通常のユークリッド空間の計量のように 「ベクトルの大きさが0」←→「ベクトルは0ベクトル」 とはなりません．(0ベクトルは任意のベクトル 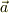に対して 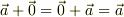が成立することで定義します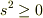．) も成り立ちません．

ですから，そういう空間で「素朴な考え」をそのまま持ってきても混乱が生じます．

> 物理的に解釈して『光はミンコフスキー空間を移動しない』ということを示し > ているのでしょうか？

ここで言う移動「しない」の定義はなんですか?

変位ベクトルが0ベクトルであると言うことですか? 変位ベクトルの「大きさ」が0であると言うことですか?

どちらで考えるかでyes/noは変わりますし，「移動」の意味も変わります． (前者は幾何学的な関係だし，後者は固有時刻の変化と解釈できますね．)