偏微分の計算

じゅんさんの書込 (2006/01/17(Tue) 19:47)

はじめまして，物理専攻の理学部の大学１年生です．電磁気のポアソンの方程式の問題です，途中経過が一応載っているのですが途中の計算で悩んでいます．

「半径Rの球内で密度ρで一様に分布した電荷による静電場をポアソンの方程式を解くことによって求めよ」

電荷の分布が中心対称だから，それによって生じるポテンシャルも中心対称で，原点からの距離のみの関数になる．それを 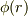$\phi (r)$ と置くと

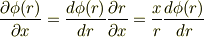
$\frac{\partial \phi (r)}{\partial x} = \frac{d \phi (r)}{d r} \frac{\partial r}{\partial x} = \frac{x}{r} \frac{d \phi (r)}{d r}$

この計算の部分なのですが左の式から真ん中の式を経て右の式に至るのかが分かりません．どうかご教授お願いします．

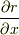微分の chain rule は良いですよね？ $\frac{\partial r}{\partial x}$ の計算ですが 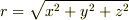$r = \sqrt{x^2+y^2+z^2}$ に注意すれば

$\frac{\partial r}{\partial x} & = \frac{\partial}{\partial x} \left(\sqrt{x^2+y^2+z^2}\right)\\& = \frac{x}{\sqrt{x^2+y^2+z^2}}\\& = \frac{x}{r}$

となります．

ありがとうございます，偏微分のchain ruleに慣れていなくって全然気づきませんでした．