量子
量子
ゆま さんの書込 (2006/01/16(Mon) 00:15)
はじめまして,物理学科の学生のゆまといいます. 量子力学の問題で, 一次元の階段型ポテンシャル,
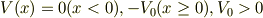
のなかをエネルギーE(E>0),質量mの粒子がx<0からx>0に向かって入射している.
このとき反射率R,x>0への透過率Tを求め, 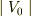 →∞の極限でのR,Tの収束値を求めよ.
というものがありました.
これをといてみたのですが,解く過程も答えも,
→∞の極限でのR,Tの収束値を求めよ.
というものがありました.
これをといてみたのですが,解く過程も答えも,
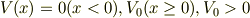
のときとまったく同じで,
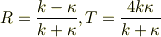
となってしまいました.
違うのは,kとκの値で,
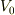 のときは,
のときは,
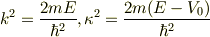
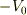 のときは,
のときは,
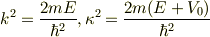
でした.
このまま,RとTの表式に代入して問題文( 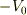 の場合)の収束値を計算すると,
の場合)の収束値を計算すると,
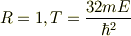
となり,おかしくなってしまいました. 本来ならR=0,T=1となるはずだと思っていたのですが…. なにが違ったんでしょう?
そして,もうひとつ疑問なのですが,
この問題文の状況の場合,直感的には 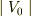 の極限操作に関わらず(つまり,RとTはk,κの表式にはならずに)初めから,R=0,T=1となると感じたのですが,そうはならないのですが?なぜ,ならないのですか?
はじめから私の解き方が違うんでしょうか?
の極限操作に関わらず(つまり,RとTはk,κの表式にはならずに)初めから,R=0,T=1となると感じたのですが,そうはならないのですが?なぜ,ならないのですか?
はじめから私の解き方が違うんでしょうか?
教えてください,お願いします.
Re: 量子
yama さんのレス (2006/01/17(Tue) 14:18)
RもTも間違っています.正しい計算では,R+T=1 になるはずです.
また,  のとき,
のとき, 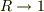 ,
, 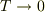 になります.
この結果は,波が伝わると考えれば,理解できるのではないでしょうか.
古典的な波動でも同じことが起こるからです.
たとえば,光が伝播速度の異なる媒質に入射するとき,表面で一部が反射されます.
反射率は,伝播速度の比が大きいほど大きくなり,伝播速度の比が極端に大きくなると1に近づきます.(ただし,光の伝播速度の比は実際には極端に大きくはなりません.)
になります.
この結果は,波が伝わると考えれば,理解できるのではないでしょうか.
古典的な波動でも同じことが起こるからです.
たとえば,光が伝播速度の異なる媒質に入射するとき,表面で一部が反射されます.
反射率は,伝播速度の比が大きいほど大きくなり,伝播速度の比が極端に大きくなると1に近づきます.(ただし,光の伝播速度の比は実際には極端に大きくはなりません.)
Re: 量子
ゆま さんのレス (2006/01/17(Tue) 15:09)
回答ありがとうございました.
計算しなおしてみて,TとRの計算は間違っていることがわかりました.
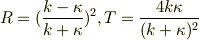
となりました.これで,R+T=1です.
これで  の収束値をとったら,
R=1,
の収束値をとったら,
R=1,  になりました.
T=0にはどうしてもたどりつけませんでした.
なにか特殊な極限操作はありますか?普通に式の全体をVで割って∞に飛ばして,Vが分母の時の値の極限値を0ととっているのではいけないのでしょうか?
になりました.
T=0にはどうしてもたどりつけませんでした.
なにか特殊な極限操作はありますか?普通に式の全体をVで割って∞に飛ばして,Vが分母の時の値の極限値を0ととっているのではいけないのでしょうか?
たしかにyamaさんのおっしゃる反射と透過の関係は古典波動でも同じなので,これが粒子がE>0で, 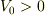 でx軸より上にあるポテンシャル壁なら,理解できるのですが,
この場合,粒子はE>0なので
でx軸より上にあるポテンシャル壁なら,理解できるのですが,
この場合,粒子はE>0なので 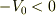 でx軸より下に井戸型に落ち込んでいるポテンシャル壁には粒子はぶつかることすらできないように思います.これはあまりに直感的に考えすぎなのでしょうか?
でx軸より下に井戸型に落ち込んでいるポテンシャル壁には粒子はぶつかることすらできないように思います.これはあまりに直感的に考えすぎなのでしょうか?
Re: 量子
ゆま さんのレス (2006/01/17(Tue) 15:13)
パスワード設定し忘れて修正できませんでした.すみません. 間違えて式が変換されていないところがあるので,正しく表示させておきます. 極限操作後の値は,
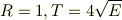
です.
Re: 量子
yama さんのレス (2006/01/17(Tue) 16:57)
Tの分子・分母を 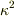 で割っておき,
で割っておき,  のとき,
のとき, 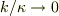 であることを用いれば,
であることを用いれば, 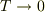 が導けます.
または,R+T=1 を用いると,R=1 ならば,T=0 であることがわかります.
古典的粒子と考えると反射するのは奇妙に思われますが,波として考えればいいのです.
この例では,伝播速度の大きい領域から,伝播速度の小さい領域に向かって入射するので,光では,たとえば空気からガラスに入射する場合に相当します.
この場合,ガラスの表面で反射がおこり,反射率は,ガラスから空気に入射する場合と等しくなります.
が導けます.
または,R+T=1 を用いると,R=1 ならば,T=0 であることがわかります.
古典的粒子と考えると反射するのは奇妙に思われますが,波として考えればいいのです.
この例では,伝播速度の大きい領域から,伝播速度の小さい領域に向かって入射するので,光では,たとえば空気からガラスに入射する場合に相当します.
この場合,ガラスの表面で反射がおこり,反射率は,ガラスから空気に入射する場合と等しくなります.