無題

無題

kkondo さんの書込 (2006/01/15(Sun) 18:37)

こんにちは．

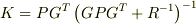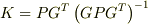さて，Kalman gain の計算 K = P G^T \left( G P G^T + R^{-1} \right)^{-1} もしくは K = P G^T \left( G P G^T \right)^{-1} におきましてなのですが，正定値対称行列 P の主値のいくつかを > ! Undefined control sequence. > \infinity とおいて計算しようとしておりますところです．

このような前例はどこかにあるでしょうか？

Re: Kalman gain

kkondo さんのレス (2006/01/16(Mon) 16:36)

こんにちは．

自分で少し考えてみました．

正定値対称行列 P の主値が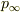， p_{\infty} （すなわち無限大）もしくは有限の正の実数なのですから，まず 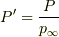P^\prime = \frac{P}{p_{\infty}} （非正則行列）を計算することにします．そして，一般逆行列を用いて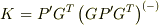， K = P^\prime G^T \left( G P^\prime G^T \right)^{(-)} と計算しました．

これで正しいでしょうか．．？