向き合う斜面の問題
向き合う斜面の問題
ぽん さんの書込 (2006/01/13(Fri) 11:04)
はじめまして.ぽんと申します. 大学の講義で分からない問題が出たので質問です.
偶然 最近の書き込みで同様の斜面についての問題が 質問されていたので そちらを参考にさせてもらってたのですが どうしても分からないのです.
問.
水平面とそれぞれA及びBの各をなす
2つの斜面が向き合っている.
第一の斜面から面に垂直な方向に投げられた物体が
第二の斜面に垂直に落下したとすれば 初速Voは
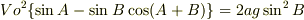 で定まることを示めせ.
ただし
で定まることを示めせ.
ただし  とは両斜面の交線から投射点までの
最短距離とする.
とは両斜面の交線から投射点までの
最短距離とする.
投射点をAをなす角の上で行うとすると
投げ上げる位置(高さ)hは 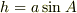 と言う事は
思いつきました.
しかし,それ以降がなかなか….
どうか よろしくお願いします.
と言う事は
思いつきました.
しかし,それ以降がなかなか….
どうか よろしくお願いします.
Re: 向き合う斜面の問題
やかん さんのレス (2006/01/13(Fri) 16:44)
ぽんさん,はじめまして!私もやってみて答えまでたどり着かず,わからないのですが
式にはtが入ってないですよね?水平面方向をx軸,垂直にy軸とすると,各成分速度 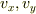 として時間t後では
として時間t後では
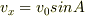
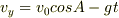 ですから,これの比(ただし,
ですから,これの比(ただし, 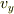 は負)が
は負)が 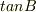 ,
もうひとつは,時間t後の位置を,例えば投げた点から水平面におろした垂線の足を原点として座標で表し,その値に,y方向の値には
,
もうひとつは,時間t後の位置を,例えば投げた点から水平面におろした垂線の足を原点として座標で表し,その値に,y方向の値には 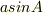 を足し,x方向の値には
を足し,x方向の値には 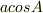 を減じて,その比がまた
を減じて,その比がまた 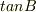 になるとおき,2つの式から,tを消去したらどうだろうと思ったのですが,いかがでしょうか?
になるとおき,2つの式から,tを消去したらどうだろうと思ったのですが,いかがでしょうか?
Re: 向き合う斜面の問題
ぽん さんのレス (2006/01/13(Fri) 22:47)
やかんさん初めまして. 返信ありがとうがございます...
なるほど比を用いてtを消去なんですか….
私は以前の斜面の問題の書き込みから
斜面に垂直で落下すると言うことを用いて
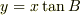 この式に運動方程式を代入して
tの式を作り,消去するものとばかり思ってました.
この式に運動方程式を代入して
tの式を作り,消去するものとばかり思ってました.
…どうなんでしょうか? 私も少しだけですが再チャレンジしてみたのですが やはり行き詰ってしまうと言うか 糸口がわからないです...
どうしたものなんでしょうか….
Re: 向き合う斜面の問題
山旅人 さんのレス (2006/01/14(Sat) 00:17)
私も,やかんさんがおっしゃる方法でただひたすら計算してみました. かなり大変な計算だったのですが,ぼんさんがあげている証明すべき式までたどり着きました.以下,概要を書きます.
(1)傾きAの斜面を左側に,傾きBの斜面を右側にし,斜面の交点を原点にとると, 投射点の座標は,(−acosA,asinA) (2)斜面に直角に投射するのだから,仰角は π/2−A (3)時間 t 後の速度 (v x ,v y ) は, v x =v 0 sinA …(#1),v y =v 0 cosA−gt …(#2) (4)時間 t 後の位置 (x,y) は, x=−acosA+v 0 sinA・t …(#3) y=asinA+v 0 cosA・t−(1/2)gt 2 …(#4)
斜面Bに直角に衝突⇔v y /v x =−1/tanB …(#5) (#5)から計算を進めると,t= (v 0 /g)sin(A+B)/sinB …(#6)
斜面Bに衝突⇔y/x=tanB …(#7)
(#7)に(#3)(#4)(#6)を代入しただひたすら計算を敢行すると, <b>v 0 2 [sinA−sinBcos(A+B)]=2agsin 2 B</b>
Re: 向き合う斜面の問題
山旅人 さんのレス (2006/01/15(Sun) 01:04)
この問題を解きながら考えたことを,書かせてください.
両斜面を,それぞれ斜面A・斜面Bとよぶことにします. 本問は,斜面A上のある点をある初速で垂直に飛び出した質点が,斜面Bに垂直に衝突します.両斜面での衝突を完全弾性衝突(e=1)とすれば,質点は衝突直前の速さで斜面Bを垂直に飛び出し,その後斜面Aに垂直に衝突します.
すなわち小球は両斜面の間を往復運動する(永久に)ことになり,“状況” は,A・Bについて “対称” なのです.飛跡は放物線なのでその一部は軸に関し左右対称ですがそういう意味ではなく.
しかしながら,本問へのアプローチのために与えられた設定(a,v 0 )は明らかに “非対称” で,このことが泥沼の計算を強いる悪の根源となっているのです.“対称性” を主眼に考えれば,もっと見通しが良くなるはずです.と考えてたどり着いたのが,以下の方法です.
質点が空中で放物運動をしている間に保存されているのは速度のx成分で,これを V とする.すると, 斜面Aを飛び出すときの速度のy成分は,VcotA …(*1) 斜面Bを飛び出すときの速度のy成分は,VcotB …(*2) よって,投射点から最高点までの時間 t A ,t B は, t A =(V/g)cotA …(*3),t B =(V/g)cotB …(*4)
原点から投射点までの距離を a,b すると,投射点間の水平距離は, acosA+bcosB=V(t A +t B )=(V 2 /g)(cotA+cotB) …(*5)
最高点の高さについて, asinA+(1/2)gt A 2 =bsinB+(1/2)gt B 2 ∴ asinA−bsinB=(V 2 /2g)(−cot 2 A+cot 2 B) …(*6)
(*5)(*6)をa,bについての連立方程式と見なして解けば,与えられた V に対する <b>投射点</b> 及び <b>投射速度</b> が導かれます.
如何でしょうか.手前味噌で恐縮ですが,私はこちらの方が問題の全体像が明解になっていると思います.
Re: 向き合う斜面の問題
やかん さんのレス (2006/01/15(Sun) 01:28)
山旅人さん,こんにちは.
>私も,やかんさんがおっしゃる方法でただひたすら計算してみました. かなり大変な計算だったのですが,ぼんさんがあげている証明すべき式までたどり着きました.
おお,考え方だけは私のでもあってたんですね.ちょっとだけ嬉しいです :)
でも,計算の手間を考えると,No8020でおっしゃっている点に気がつくかどうかが,出題の意図なのかもしれませんね(さすが大学の問題!). 私も勉強になりました. ぽんさん,解決になりそうで良かったですね :)
Re: 向き合う斜面の問題
ぽん さんのレス (2006/01/16(Mon) 08:52)
山旅人さん初めまして. そして 山旅人さんやかんさんありがとう御座いました.
難しいですね… そのようなところまで気がつきませんでした.
でもようやく理解することが出来そうです. 本当にありがとうございました.
Re: 向き合う斜面の問題
ぽん さんのレス (2006/01/25(Wed) 00:47)
せっかく回答してくださったのですが ここ数日頑張っても与えられた式に辿り着かないんです…. 山旅人さんの解説の#7に#3,#4,#6を代入して計算を進めると
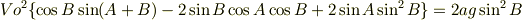
…書くだけでも大変でしたが,ここまでは辿り着きました…. 左辺の()内の整理だけなのですが…. 物理ではなく ただの数学の世界かも知れませんがヒントだけでも お願いいたします...
追記:最初の投稿の物は誤ったものでした.お詫びして訂正します.
Re: 向き合う斜面の問題
やかん さんのレス (2006/01/25(Wed) 19:27)
ぽんさん,頑張っていらっしゃいますね! :)
ちょっと姑息な方法ですが,この問題は”・・・となることを示せ”ですから 左辺の中括弧の中身同士を,ぽんさんが出された物から,問題文の物を 引いてゼロになればいいですよね.今やってみたのですが,両方,加法定理で (A+B)の括弧をはずして計算すると,確かにゼロになりました.
Re: 向き合う斜面の問題
ぽん さんのレス (2006/01/25(Wed) 21:25)
やかんさん ありがとうございます!! 出来ました!一緒に悩んでた同級生一同スッキリしました. ようやくこの問題も終われます...
Re: 向き合う斜面の問題
やかん さんのレス (2006/01/26(Thu) 15:01)
ぽんさん,解決して良かったですね☆ 私もぽんさんと山旅人さんのおかげで勉強になりました. これから寒くなりますがお体に気をつけて頑張って下さいね! :)