無題
無題
みかん さんの書込 (2006/01/11(Wed) 09:28)
はじめまして 高校生のみかんと申します. 物理の授業で分からない問題が出てきて困ってます. どなたか教えていただけないでしょうか?
問題は,地表で初速Voで投げ出された物体の水平到達距離を 同じ初速で鉛直上方に投げたときの最高点の高さに等しくするには どの方向になげればいけないか?というものです.
投げ上げ運動と放物線運動の運動方程式を立てて, 代入法で解いてみたのですが, 最後がsinθ=1 θ=90°となってしまい, 結局 鉛直方向の投げ上げになってしまいます. どのようなとき方をすればよいのでしょか...
Re: 無題
やかん さんのレス (2006/01/11(Wed) 22:00)
みかんさん,はじめまして!頑張ってますね. せっかくですから,みかんさんが立てて解いた運動方程式を 書いてみてもらえますか?そうすれば式の間違いか,計算間違いか(もし間違っていればですけど)がわかると思いますよ :)
Re: 無題
みかん さんのレス (2006/01/11(Wed) 23:04)
やかんさん初めまして. 返信ありがとうございます.
立てた運動方程式は 鉛直方向が h=-(1/2)gt^2+Vot 水平方向が x=-(1/2)gt^2+(Vo sinθ)t です.
hとxが等しくなるので -(1/2)gt^2+Vot=-(1/2)gt^2+(Vo sinθ)t Vot=(Vo sinθ)t Vo=Vo sinθ sinθ=1 θ=90°
…こんな形なんですけど,いかかでしょうか? どこが間違ってるか教えていただきたいです...
Re: 等加速度運動の問題
tomo さんのレス (2006/01/12(Thu) 01:00)
みかんさん,こんばんは. tomoです.
問題文をよく読みましたか?
> 地表で初速Voで投げ出された物体の水平到達距離を > 同じ初速で鉛直上方に投げたときの最高点の高さに等しくする
です.「水平到達距離」と「最高点」を正しく理解していますか.
投げ出す点を原点に取り,鉛直方向上向きを  軸の正,
水平方向右向きを
軸の正,
水平方向右向きを  軸の正とし,投げ出した時を時刻
軸の正とし,投げ出した時を時刻  とします.
角度
とします.
角度  方向に投げ出された物体の
方向に投げ出された物体の  秒後の
秒後の
 座標を
座標を 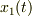 ,
,  座標を
座標を 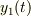 ,
,  方向の速度を
方向の速度を 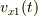 ,
,  方向の速度を
方向の速度を 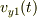 とし,
鉛直上向きに投げ出された物体の
とし,
鉛直上向きに投げ出された物体の  秒後の
秒後の
 座標を
座標を 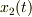 ,
,  座標を
座標を 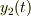 ,
,  方向の速度を
方向の速度を 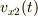 ,
,  方向の速度を
方向の速度を 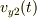 とします.
とします.
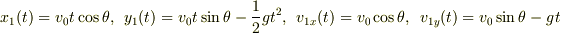
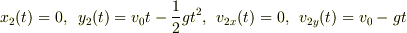 という8つの式が立てられるところまではOKでしょうか.
という8つの式が立てられるところまではOKでしょうか.
上4つの式から,角度  方向に投げ出された物体の水平到達距離
方向に投げ出された物体の水平到達距離  を計算してください.
(投げ出した後,再び地面に落ちる時刻を求め,その時刻の
を計算してください.
(投げ出した後,再び地面に落ちる時刻を求め,その時刻の  座標を求めます.)
次に下4つの式から,鉛直上方に投げ出された物体の最高点の高さ
座標を求めます.)
次に下4つの式から,鉛直上方に投げ出された物体の最高点の高さ 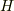 を計算してください.
(投げ出した後,最高点に達する時刻を求め,その時刻の
を計算してください.
(投げ出した後,最高点に達する時刻を求め,その時刻の  座標を求めます.)
座標を求めます.)
最後に, 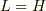 とすれば,求める
とすれば,求める  が出てきます.
がんばってください :)
が出てきます.
がんばってください :)
#1 「hとxが等しくなるので」というところが違っています.勘違いかもしれません. #2 掲示板に書き込む際は,適当なタイトルを付けましょう.
Re: 等加速度運動の問題
やかん さんのレス (2006/01/12(Thu) 19:03)
tomoさん,有難うございます.高校の内容だったのでついレスを書いたのですが,心細かったので助かりました (^^;(4番目の式はサインでしょうか?) みかんさん,頑張って下さいね.レス遅くなってすみませんm(__)m
Re: 等加速度運動の問題
tomo さんのレス (2006/01/12(Thu) 22:18)
やかんさん,こんばんは.
ご指摘ありがとうございました.修正しました. ミスなく書ける自信ないなぁと思って書いたら,案の定でした (^^;
Re: 等加速度運動の問題
みかん さんのレス (2006/01/12(Thu) 23:12)
tomoさん,やかんさんありがとうございました. 次からはちゃんとタイトルつけますね.
やっぱ無茶に解こうとしてたんですね...
自分で今から解いてみます!