除去できる特異点を持つ関数のテーラー展開
除去できる特異点を持つ関数のテーラー展開
ゆうぅ さんの書込 (2005/12/31(Sat) 15:25)
大学で物理を学んでいる者です. どうしても分からないことがあるので,質問させてください. f(z)=z/{exp(z)-1} は,z=0が除去可能な特異点になっているのでz→0でf(0)を定義しなおすことによって,f(z)を連続な関数と見なすことができることは分かるのですが,それではこのf(z)はz=0のまわりでテーラー展開できるのでしょうか?もしできるのなら,どうかやり方を教えてください.
Re: 除去できる特異点を持つ関数のテーラー展開
篠原 さんのレス (2005/12/31(Sat) 18:16)
ゆうぅさん,はじめまして. 篠原です.
私はあまり解析学が得意ではないので,あっているかわかりませんが,テイラー展開できると思います. テーラー展開は,ご存知のとおり
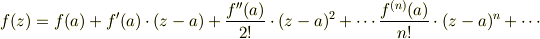
ですよね.これにa=0を代入し,f(0)は,z→0としたときのf(z)の値を使えば良いのではないでしょうか. 極限の値はロピタルの定理などからすぐに求まりますよね.
数学は,それほど自信は無いので,間違っていたらごめんなさい.
あと,ゆうぅさん,
このサイトでも同じ質問をされていますね. マルチポストは,マナー違反だと考える人もいます(私もその一人です) 気をつけたほうが良いですよ.
Re: 除去できる特異点を持つ関数のテーラー展開
ゆうぅ さんのレス (2006/01/10(Tue) 12:00)
返信ありがとうございます. もし,極限の値が0であったときにはf(z)=0になってしまいますが,こういうときはどうしたらいいのでしょうか?
掲示板を使って質問することは滅多になかったので,マナーをよく知りませんでした.今後気をつけたいと思います..
Re: 除去できる特異点を持つ関数のテーラー展開
黒子 さんのレス (2006/01/10(Tue) 22:12)
はじめまして,ゆうぅさん. 私も返事を書いていながら,数学はそんなに得意ではないんです. なので,ゆうぅさんの質問にそぐわないことを書いていたらすいません.
 で
で 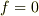 になっても,
になっても,
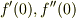 では
では  になるわけではありません.
なので,篠原さんの書いてくださった定義式のように計算すれば,
になるわけではありません.
なので,篠原さんの書いてくださった定義式のように計算すれば,
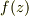 は何かしらの関数になると思います.
は何かしらの関数になると思います.