勝大 さんの書込 (2005/12/25(Sun) 13:56)

はじめまして．工学部1年の勝大(かつひろ)と申します． 授業で力学の講義があるのですが，冬季休業・後期の考査が目前に 迫ってきた事もあり，講義のたびに難題が次から次に出題されてます…． 自力で調べたり，友達と協力して7問の内 4問は解決しました． 5問目でつまづいてしまってます．よろしくお願いします．

Q. 水平面と角θをなす斜面状上の一点Oから斜面と垂直に交わる 鉛直面内で投げ上げられた質点が斜面上の点に垂直に当たるには 斜面に対して どの様な角度で投げ上げなければならないか？ 但し，空気抵抗・浮力は考えない物とする．

横軸をx(右向き正)，縦軸をy(上向き正)として運動方程式を立てて 運動曲線を求めることは出来ました． また質点が到達し得る最高点も出すことは出来るのですが 角度に由来する問題に関してはわからなくて…．

ご回答頂けたら幸いです．よろしくお願いします．

山旅人 さんのレス (2005/12/25(Sun) 23:01)

初めまして，山旅人と申します．お尋ねの問題は，素直に計算すればできますよ．

初速度 Ｖ，仰角 α で投げ上げるとき，時間 ｔ 後の速度 Ｖ _x ，Ｖ _y ，位置 ｘ，ｙ は， Ｖ _x ＝Ｖｃｏｓα … (1)Ｖ _y ＝Ｖｓｉｎα−ｇｔ … (2) ｘ＝Ｖｃｏｓα・ｔ … (3)ｙ＝Ｖｓｉｎα・ｔ−(１/２)ｇｔ ² … (4)

傾斜 θ の斜面に落下 ⇔ ｙ＝ｘｔａｎθ … (5) (3)(4)を(5)に代入し，落下時刻はｔ＝(２Ｖ/ｇ)(ｓｉｎα−ｃｏｓαｔａｎθ) … (6)

斜面と垂直に当たる ⇔ Ｖ _y /Ｖ _x ＝−１/ｔａｎθ… (7) (1)(2)(6)を(7)に代入し整理整頓すると ｔａｎα＝<b>２ｔａｎθ＋１/ｔａｎθ</b>…［答］

勝大 さんのレス (2005/12/27(Tue) 15:35)

山旅人さん ありがとうございました． 本当に助かりました．

残り2問頑張っていきます．．．

勝大 さんのレス (2006/01/10(Tue) 23:13)

すみません 再び行き詰ってしまい質問です…．

Q. 速度に比例する抵抗(-kv)があるとき 鉛直上方に地表から初速度Voで投げ上げられた 質点(質量m)の運動を求めよ．

かかる力が上向き正として 負の方向に重力加速度と抵抗の力が加わり 正の方向に鉛直投げ上げの運動がかかるのは 分かるのですが， 問題が漠然としすぎていて いまいち掴みきれません． どうか解説のほうよろしくお願いいたしますm(_ _)m

山旅人 さんのレス (2006/01/11(Wed) 20:54)

運動方程式ｍｄＶ/ｄｔ＝−（ｍｇ＋ｋＶ） …… (1) (1)を解いて，一般解は，Ｖ＝−ｍｇ/ｋ＋Ｃｅｘｐ（−ｋｔ/ｍ） …… (2) ｔ＝０ のとき Ｖ＝Ｖ ₀ だから，Ｃ＝Ｖ ₀ ＋ｍｇ/ｋ

∴ <b>Ｖ＝−ｍｇ/ｋ＋（Ｖ ₀ ＋ｍｇ/ｋ）ｅｘｐ（−ｋｔ/ｍ）</b> …… (3)

勝大 さんのレス (2006/01/12(Thu) 23:04)

山旅人さん 2度も回答 本当にありがとうございました． 回答を見ながら考え直してみます．

山旅人 さんのレス (2006/01/12(Thu) 23:40)

「（１）を解く」過程を省いてしまいました．

運動方程式ｍｄＶ/ｄｔ＝−（ｍｇ＋ｋＶ） …… (1)

これより， ｍｄＶ/（ｍｇ＋ｋＶ）＝−ｄｔ …… (２) 両辺を積分すると （ｍ/ｋ）ｌｏｇ（ｍｇ＋ｋＶ）＝−ｔ＋Ｃ' …… (３) ∴ ｌｏｇ（ｍｇ＋ｋＶ）＝−（ｋ/ｍ）（ｔ＋Ｃ'） ∴ ｍｇ＋ｋＶ＝ｅｘｐ［−（ｋ/ｍ）（ｔ＋Ｃ'）］ ＝Ｃ''ｅｘｐ［−（ｋｔ/ｍ）］（Ｃ''＝ｅｘｐ［−（ｋ/ｍ）Ｃ'］） ∴ Ｖ＝−ｍｇ/ｋ＋Ｃｅｘｐ（−ｋｔ/ｍ）（Ｃ＝Ｃ''/ｋ）←一般解

この後は，上記の通りです．

勝大 さんのレス (2006/01/20(Fri) 16:46)

山旅人さん 遅れながら 回答ありがとうございました．

失礼ながら質問なのですが (1)式より両辺を積分してmV=-(mg+kV)t+C 初期条件はt=0でV=VoなのでC=mVo よって V=-{(mg+kV)/m}t+Vo 運動方程式は両辺を積分して y=-{(mg+kV)/2m}t^2+Vot+C' 初期条件はt=0でy=0なのでC'=0 よって求める運動方程式は ∴y=-{(mg+kV)/2m}t^2+Vot

これは間違いなのでしょうか？

ご回答下さったら幸いです．

山本明 さんのレス (2006/01/20(Fri) 17:37)

勝大さん，はじめまして． 山旅人さんではありませんが，

>(1)式より両辺を積分してmV=-(mg+kV)t+C

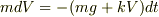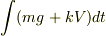ここが違います．もとの微分方程式から として，両辺を積分する…という発想だと思いますが，右辺の は時間と共に変化します．だから単純に積分をしようとしても， は 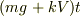にはなりません ( が の関数だからです)．

先の山旅人さんの回答だけで十分かもしれませんが，物理のかぎしっぽにも抵抗ありの落下運動についての解説がありますので，よろしければ参考にしてみてください．

• http://www12.plala.or.jp/ksp/mechanics/resistdown/index.html
• http://www12.plala.or.jp/ksp/mechanics/fallInAirResistance/index.html