2変数の連立方程式
2変数の連立方程式
みぃ さんの書込 (2005/12/24(Sat) 20:45)
はじめまして.工学部3年に在籍してますみぃです.よろしくお願いします. 先日,実験がありまして,その過程で次の2式の連立方程式を解けという問題が出てきました.
I(d 2 θ 2 /dt 2 )+Lmgθ 2 +k 1 <i>l</i> 2 θ 2 +k 2 <i>l</i> 2 (θ 2 -θ 1 )=0 I(d 2 θ 1 /dt 2 )+Lmgθ 1 +k 1 <i>l</i> 2 θ 1 +k 2 <i>l</i> 2 (θ 1 -θ 2 )+k 0 <i>l</i> 0 2 =k 0 ><i>l</i> 0 <i>r</i>cosωt
この2式です. また,θ 1 =θ 10 cosωt θ 2 =θ 20 cosωtで,表せます. あと,I,L,m,g,k 0 ,k 1 ,k 2 ,<i>l</i>,<i>l</i> 0 ,<i>r</i>は全て定数で,次のように与えられています. I=0.0173 L=0.24 m=1.84 g=9.8 k 0 =108.4 k 1 =548.7 k 2 =737.2 <i>l</i>=0.182 <i>l</i> 0 =0.07
このときのθ 10 ,θ 20 が最大になる条件を求めて,ωとθ 10 ,θ 20 を求めよ. ・・・との事なんです... 自分でもやってみたのですが,4階微分方程式(?)みたいになって,それにcosやsinがついたりで,よくわかりません・・・ 値を代入しなくてもいいので,どなたかわかりましたらご教授の程,よろしくお願いします.
すみません・・・追加します^^;
みぃ さんのレス (2005/12/24(Sat) 20:57)
すみません・・・ 見にくいですね^^;
えっと,kの次に書いている文字はl(エル)です・・・ kl 2 θや,k 0 l 0 rcosωtみたいな感じです. あ,あとk 0 >l 0 rcosωtなどと書いてますが,k 0 l 0 rcosωtの間違いです.すみません^^; それとr=0.0048で与えられていました.何度も申し訳ありません・・・
ご教授の程,よろしくお願いします☆
Re: 2変数の連立方程式
tomo さんのレス (2005/12/24(Sat) 23:49)
みぃさん,こんばんは. tomoです.
> 自分でもやってみたのですが,4階微分方程式(?)みたいになって,それにcosやsinがついたりで
ご自分でやってみた過程と結果を書いてみてはいかがでしょうか. その方がレスが付きやすいと思います.がんばってください :)
Re: 2変数の連立方程式
みぃ さんのレス (2005/12/25(Sun) 03:08)
tomoさん.レスありがとうございます!! そうですね^^一応私はこうなりました.
まず,1式目をθ 10 =の形にして,それを2式目に代入し,定数も全て代入して計算したところ,このようになりました.(合っているかどうかわかりませんが・・・)
0.0000505(d 4 θ 20 /dt 4 )cosωt-0.000202(d 3 θ 20 /dt 3 )ωsinωt-(0.1706-0.000202ω 2 )cosωt-0.3412(dθ 20 /dt)ωsinωt-(0.0000505ω 4 +0.17061ω 2 +66.762)θ 20 cosωt-0.0364224cosωt=0
ここからどうすればθ 20 が最大になる条件がわかりますか?もしくはθ 20 について解くことが出来ますか? sinやcosがついていてどうすればいいのかわかりません・・・ sinやcosがなかったらわかりやすいのに・・.
あぁ〜これが終わらないとクリスマスが台無し・・・^^;
Re: 2変数の連立方程式
崎間 さんのレス (2005/12/25(Sun) 08:11)
微分方程式に単純に代入,というのは変です.
僕もちょっと分からなくて気になったので考えてみました.
まず与えられた式を整理します.
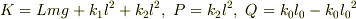 と置き,
2階微分を
と置き,
2階微分を 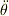 のようにドットを二つ付けて表すと
のようにドットを二つ付けて表すと
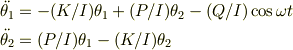
となります.これを行列で表すと
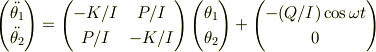
となります.あとは,なんとかして固有値と固有ベクトルをもとめてやれば
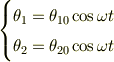
の形になって 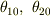 の値が具体的にもとまるのではと思います.
の値が具体的にもとまるのではと思います.
Re: 2変数の連立方程式
みぃ さんのレス (2005/12/25(Sun) 09:18)
崎間さん.おはようございます^^レスありがとうございます. 早速やってみているのですが,どうもうまくいきません・・・ この行列式を解けばよいのですか? あまり行列は得意な方ではないので,よろしかったら少しでいいので解法ののヒントを頂けないでしょうか? よろしくお願いします...
Re: 2変数の連立方程式
崎間 さんのレス (2005/12/25(Sun) 09:57)
http://atmori.hp.infoseek.co.jp/matx/diffeq/
など参考になるのではと.あ,
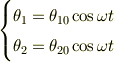
が分かっているので,先にこれを代入した方がいいです.
Re: 2変数の連立方程式
みぃ さんのレス (2005/12/25(Sun) 10:24)
崎間さん.何度もレスありがとうございます^^ えっと,その行列の前の2式に<b>θ 1 =θ 10 cosωt</b>と<b>θ 2 =θ 20 cosωt</b> を代入するのですよね? やはり計算すると4階微分方程式になってしまうのでしょうか??
Re: 2変数の連立方程式
みぃ さんのレス (2005/12/25(Sun) 13:20)
すみません・・・ リンクのほう参考にさせて頂きました.
リンクの方法と同じように,<i>(θ 1 +θ 2 )</i>と,<i>(θ 1 +θ 2 )</i>でくくってみました. そのあとω=の形になっていて,それと同じようにやりたいのですが,<i>-(Q/I)cosωt</i>があるのでわかりにくいです... ωのルートのなかに<i>-(Q/I)cosωt</i>も入ってしまうのでしょうか?
何度も何度もごめんなさい・・・・・・
Re: 2変数の連立方程式
崎間 さんのレス (2005/12/25(Sun) 14:19)
> 同じようにやりたいのですが,-(Q/I)cosωtがあるのでわかりにくいです...
ですね.-(Q/I)cosωtがじゃまっすよね! これは外力の加わった連成振動の問題でしょうか. 僕も解答をもっているわけではないんで, ちょっと怪しいですがつづきを書いてみます.
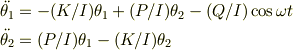
に
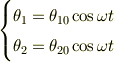
を代入すると
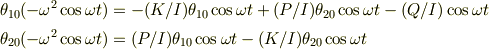
になります.あとは両辺の 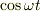 を払って,
を払って,
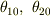 について連立方程式を解いて求めればいいのではないかなぁ
(
について連立方程式を解いて求めればいいのではないかなぁ
( 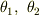 の解の形が知られているため,
連立の2階微分方程式が単なる連立方程式になったわけです).
途中計算は
の解の形が知られているため,
連立の2階微分方程式が単なる連立方程式になったわけです).
途中計算は
が参考になると思います(今見つけました,出し惜しみじゃないです :) ).
Re: 2変数の連立方程式
みぃ さんのレス (2005/12/25(Sun) 21:38)
レス遅れてすみません・・・ 崎間さん本当にありがとうございます!!
・・・大変言いにくいのですが,実は先ほど,問題の間違いに気づいてしまいました・・・ 2式目の=の左にk 0 l 0 2 とありますが, k 0 l 0 2 <b>θ 1 </b>の間違いでした・・・ KやQで置いたところがダメになってしまいましたね・・・
崎間さん.大事な休みの日に付き合ってもらって本当にありがとうございました. あとは自分で何とかしてみます! もし,お暇でしたら手伝って頂けるとありがたいです. 本当にありがとうございました!!