静電ポテンシャル

home > 掲示板 >

このページのPDF版

サイトマップ

静電ポテンシャル

あおいさんの書込 (2005/12/22(Thu) 12:27)

理学部1年在籍のあおいと申します．電磁気学は学び始めてまだ2ヶ月程度です．

授業で以下のような問題が出ました．「rotE↑=0↑⇔E↑=-gradφ を示せ．」 (E↑：電場φ：静電ポテンシャル)

右から左は示すことができたのですが，左から右を示すことがどのようにやればよいのかまったくわかりません．

いろいろと調べてみたのはいいのですが， [rot が 0 となる場は，何らかのスカラー場の gradで表現できる]…(*) と書いてあるばかりで，答えに行き着くことは出来ませんでした．出来ましたら，電場に限らず一般に(*)が成り立つこともご教授願いたいと思います．

どうぞよろしくお願いします．

Re: 静電ポテンシャル

渡邉さんのレス (2005/12/22(Thu) 17:22)

どうもはじめまして．学部3年ですが，僕も rotE↑=0↑→E↑=-gradφ の証明をした事無いです．（多分）で，テキトーに考えたのですが．まずこれの対偶は「E↑≠-gradφ →rotE↑≠0↑」ですね．これを示せば，証明になります．つぎに左の式のrotをとってみてください．rotE↑≠0↑が得られます． (←を示すときにrotgrad φ=0は示されたものとして考えています)

以上ですが，よく検討してくださいね．正しいとは限りません．もちろん，僕は正しいと思い込んでいますが．

一般論についてですが，この（←）の証明にも，E↑は，ベクトル場．φは任意関数である条件しか使っていないはずです．だからE↑電場，φ電位である必要は無いというだけですよ．

*NO.7777！！！7が4つ．これは，何かあるな！？（謎）

Re: 静電ポテンシャル

やかんさんのレス (2005/12/22(Thu) 20:35)

あおいさん，はじめまして！渡邉さん，こんばんは！

ちょっと思いついたのですが，背理法っぽく，

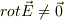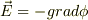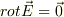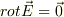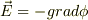$rot \vec{E} \neq \vec{0}$ の時， $\vec{E}=-grad \phi$ であらわせたと仮定すると， $rot \vec{E}= \vec{0}$ となることから（これは納得済みなので），仮定に反する．ゆえに $rot \vec{E}= \vec{0}$ のときのみ， $\vec{E}=-grad \phi$ と表せる，というのはどうでしょう？間違ってるかもしれません・・・．

＞*NO.7777！！！7が4つ．これは，何かあるな！？（謎）

うわっ，見事ですね！ :)

Re: 静電ポテンシャル

山旅人さんのレス (2005/12/22(Thu) 23:26)

“スカラーポテンシャル” で検索するとたくさんヒットします．いくつか見た中で，私がわかりやすいかなと思うのは，

スカラーポテンシャル http://www.moge.org/okabe/temp/elemag/node18.html ポテンシャル - Wikipedia http://ja.wikipedia.org/wiki/%E3%83%9D%E3%83%86%E3%83%B3%E3%82%B7%E3%83%A3%E3%83%AB

です．どうぞ，いろいろなところをご覧ください．

Re: 静電ポテンシャル

渡邉さんのレス (2005/12/24(Sat) 10:27)

やかんさん，お久しぶりです．

証明の事ですが，やかんさんの証明された命題は「rotE↑≠0⇒E↑≠-grad φ」だと思います．これは示したい命題の裏で，一般に命題と両立はしないです．

Re: 静電ポテンシャル

横槍ですが，さんのレス (2005/12/24(Sat) 15:46)

まず，No.7777の渡邉さんの指摘は正しくないと思います． ≠を使ったこのような式変形は間違っていると思います．

たとえば，ｙ＝２ｘ，ｚ＝２ｘ＋３のとき，ｙ≠ｚですが，dy/dx＝dz/dxだからです．

山旅人さんが紹介されている

http://www.moge.org/okabe/temp/elemag/node18.html のページの

上から４行目の「以上の結果，二点間を結ぶ曲線に沿う静電場の線積分は，曲線の形によらず一定になる．」という部分が大事で，よって,rotE＝０ならば線積分が定義できるので，-ΦをEの線積分と定義することができ，このΦはE＝−gradΦを満たす．

となるのだと思います．

Re: 静電ポテンシャル

渡邉さんのレス (2005/12/24(Sat) 19:05)

なるほど．言われている事は，全くその通りです．間違っているかどうかは，僕にはもう少し考える必要があります．それは，y,zが任意関数である事と，E↑が全く任意なのに対してgradφは grad(・)である事の差があるからです．

rotgrad(・)=0を考えれば，僕の証明は正しいと思います．しかし，それでも考慮してない点がある気がします．

このラインで考えれば，微分形での完全な証明が作れると思うのですが．反感をかうようでしたら，撤退します．

Re: 静電ポテンシャル

やかんさんのレス (2005/12/24(Sat) 19:25)

渡邉さん，ご指摘有難うございます．

＞証明の事ですが，やかんさんの証明された命題は「rotE↑≠0⇒E↑≠-grad φ」だと思います．これは示したい命題の裏で，一般に命題と両立はしないです．

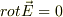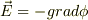うう，違ってたか・・・．すみません・・・． (^^; また違ってたら教えてくださいね :) あっ，よく考えると確かに違ってました！ $rot \vec{E}=0$ の時 $\vec{E}=-grad \phi$ である事を全然証明してませんでしたね．裏とか対偶って，高校で確かに習った気が．一度ちゃんと復習しないとなあ・・・．

Re: 静電ポテンシャル

横槍ですが，さんのレス (2005/12/24(Sat) 23:02)

確信があるわけではありませんが，今のところ僕には渡邊さんの言っていることは違うように思えます．

渡邊さんがやかんさんに指摘されているように，逆や裏が成り立ってもその命題が成り立つとは限りません．また，質問者はこのことを考えた上で質問しています．

そして，渡邊さんの証明の中では示したい内容の逆である E↑=-grad φ→rotE↑=0↑ しか使っていないように思えます．

これを利用するのはいいのですが，これしか使わずに証明できてしまうことに違和感を感じます．

ちなみに一切反感はもっていません．

Re: 静電ポテンシャル

渡邉さんのレス (2005/12/24(Sat) 23:49)

>そして，渡邊さんの証明の中では示したい内容の逆である E↑=-grad φ→rotE↑=0↑ しか使っていないように思えます

僕の書いた文章は，示したい命題「rotE↑=0↑⇒E↑=-grad φ」の対偶のつもりで書きました．しかし「∃(x↑)E↑（ｘ↑）≠-grad φ（ｘ↑）⇒∃(x↑)rot E↑（ｘ↑）≠0 」が正しい対偶だと思います．これを示すのに，左の両辺のrotをとることによって右が得られるのは明らかでしょう．

「対偶が真ならば，その命題は常に真」だという事に基づいて証明をしようという方針でいます．横槍さん（と呼ばせていただきます）の指摘は示したい命題の取り違えかと思います．

もちろん

>山旅人さんが紹介されている

http://www.moge.org/okabe/temp/elemag/node18.html のページの

上から４行目

が標準的であるし，僕の考えている方針はナンセンスかもしれませんが．（挑戦してみたくなってしまいました．意識的にこの方法を避けて，失敗した形になっているような・・・）

Re: 静電ポテンシャル

横槍ですが，さんのレス (2005/12/25(Sun) 03:20)

>僕の書いた文章は，示したい命題「rotE↑=0↑⇒E↑=-grad φ」の対偶のつもりで書きました．しかし「∃(x↑)E↑（ｘ↑）≠-grad φ（ｘ↑）⇒∃(x↑)rot E↑（ｘ↑）≠0 」が正しい対偶だと思います．

渡邊さんと僕の間に問題の認識に違いがあるようです．ぼくは渡邊さんの方に命題の取り違えがあるとおもいます．ぼくは正確に書くならば次のようになると考えています．

示したい命題は「rotE↑=0⇒∃(φ)：E↑=-grad φ」（rotE↑=0ならばE↑=-grad φを満たすφが存在する）

であり，その対偶は「∀(φ)：E↑≠-grad φ⇒rot E↑≠0 」（全てのφに対しE↑≠-grad φならば（つまりどんな関数φを考えても-gradφでE↑をあらわすことが不可能ならば）rot E↑≠0）

だとおもいます．もともと電磁気の問題なのでこの解釈で間違いないと思います．

＞挑戦してみたくなってしまいました．確かにあの証明はことばで説明した「言いたいことはわかるでしょ?」的な証明で，数式で書いたもっときれいな証明がほしいとは僕も思います．

Re: 静電ポテンシャル

渡邉さんのレス (2005/12/25(Sun) 08:57)

>示したい命題は「rotE↑=0⇒∃(φ)：E↑=-grad φ」（rotE↑=0ならばE↑=-grad φを満たすφが存在する）

であり，その対偶は「∀(φ)：E↑≠-grad φ⇒rot E↑≠0 」

なるほど．ところで，「ぼくが命題を取り違えているのでは．」と書いたのは，僕が書いた対偶命題を逆だと仰っていると勘違いしたためです．すみません．

対偶命題の左の式の両辺rotをとったら，証明にはなりませんか？ここが引っかかるとの事ですが，恒等式rotgrad(・)＝０自体が逆命題というわけではないです．だから使って良いものだと思います．

あと，僕が以前書いたものは，無意識のうちに∃(φ)を書き忘れてました．つまり僕の感覚では示したい命題は「∀x↑∈R^{3} rotE↑(x↑)=0⇒∀x↑∈R^{3}∃(φ)：E↑(x↑)=-grad φ(x↑)」

であり，その対偶は「∃x↑∈R^{3} ∀(φ)：E↑(x↑)≠-grad φ(x↑)⇒∃x↑∈R^{3} rot E↑(x↑)≠0 」

という事です．

ところで，考えていくうちに少々計算しても，直接的に証明する方法の方が良いように思えてきました．（やかさんが，下に書かれているものです．）

Re: 静電ポテンシャル

やかんさんのレス (2005/12/25(Sun) 12:46)

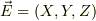
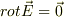家にあった書籍“ベクトル解析の基礎”（水本久夫著培風館）に載っていたのですが（以下，文字を変えて引用FをE，Uを $\phi$ ） $\vec{E}=(X,Y,Z)$ $rot \vec{E}=\vec{0}$ なら

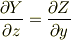
$\frac{\partial Y}{\partial z}=\frac{\partial Z}{\partial y}$

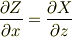
$\frac{\partial Z}{\partial x}=\frac{\partial X}{\partial z}$

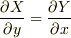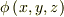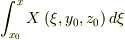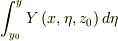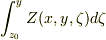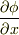
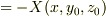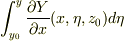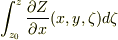$\frac{\partial X}{\partial y}=\frac{\partial Y}{\partial x}$ であり， $\phi \left( x,y,z \right)$ =- $\int_{x_0}^{x} X \left( \xi ,y_{0},z_{0} \right) d \xi$ - $\int_{y_0}^{y} Y \left( x, \eta ,z_{0} \right) d \eta$ - $\int_{z_0}^{y} Z(x,y, \zeta )d \zeta$ と定義すると $\frac{\partial \phi}{\partial x}$ $=-X(x,y_{0},z_{0})$ - $\int_{y_0}^{y} \frac{\partial Y}{\partial x}(x,\eta,z_{0})d \eta$ - $\int_{z_0}^{z} \frac{\partial Z}{\partial x}(x,y, \zeta )d \zeta$ =- $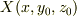X(x,y_{0},z_{0})$ - $\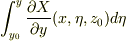int_{y_0}^{y} \frac{\partial X}{\partial y}(x, \eta ,z_{0})d \eta$ - $\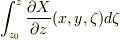int_{z_0}^{z} \frac{\partial X}{\partial z}(x,y, \zeta )d \zeta$ =- $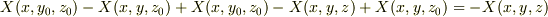X(x,y_{0},z_{0})-X(x,y,z_{0})+X(x,y_{0},z_{0})-X(x,y,z)+X(x,y,z_{0})=-X(x,y,z)$ 同様に $\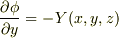frac{\partial\phi}{\partial y}=-Y(x,y,z)$ $\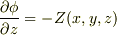frac{\partial\phi}{\partial z}=-Z(x,y,z)$ ゆえに $\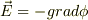vec{E}=-grad \phi$ という証明が載っていました．お話に出ている積分形と同じ事なのかなとも思いましたが，途中で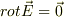， $rot \vec{E}=\vec{0}$ から得られる成分の式を使っているので，別な物かなとも思い，書いてみました．私が理解して書いているか，ただの丸写しに過ぎないか，微妙ですが，偏微分する事を前提に， $\phi$ を積分形に書いて定義し，途中で $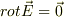rot \vec{E}=\vec{0}$ から得られる成分の式を使って変形している事はかろうじてわかりました・・・．

Re: 静電ポテンシャル

横槍ですが，さんのレス (2005/12/25(Sun) 23:37)

>対偶命題の左の式の両辺rotをとったら，証明にはなりませんか？ここが引っかかるとの事ですが，恒等式rotgrad(・)＝０自体が逆命題というわけではないです．だから使って良いものだと思います．

使ってよいと思います

ただ，「∀(φ)：E↑≠-grad φ⇒rot E↑≠0 」の左の式のrotをとっても簡単には証明できないと思います．仮に，rot A↑（ｘ↑）＝０を満たすA↑（ｘ↑）でgradφという形で表すことの出来ないものが存在するとします．そう仮定すると「∀(φ)：E↑≠-grad φ」であったとしても，E↑＝A↑とおくことでrot E↑＝0とすることが出来ます．つまり，このようなA↑（ｘ↑）は存在しないことが先に示されていないと証明できません．これは「rotE↑=0⇒∃(φ)：E↑=-grad φ」がわかっていないといけないということと同じことだと思います．

つまり，この両辺のrotをとることで命題の待遇を証明する方法には，あらかじめ元の命題を証明しておく必要があるのではないか？と感じているということです．

やかんさんの方法を答えれば正解になりそうですね．

Re: 静電ポテンシャル

横槍ですが，さんのレス (2005/12/26(Mon) 01:02)

ぼくが最も主張したかったことを簡単に表現できることに気づいたので書きこみます．

ｙ＝ｚ⇒φ（ｙ）＝φ（ｚ）と考えてもよいが，ｙ≠ｚ⇒φ（ｙ）≠φ（ｚ）となるとは限らない．ということです．これはｙ，ｚが変数であろうと，関数であろうと，正しいだろうと思っています．

（多価関数の場合は少し話が複雑になりますが，集合の写像として考えれば，上のことがなりたつと考えています．ただ，ここはそんなに自信が無いのでとりあえずそうではない普通の写像を考えてください．（単射という言葉を間違って用いてしまったので訂正しました．））

Re: 静電ポテンシャル

渡邉さんのレス (2005/12/26(Mon) 11:41)

ようやくこの証明が分かりました．ありがとうございます．

Re: 静電ポテンシャル

ｙama さんのレス (2005/12/26(Mon) 15:18)

No.7819に渡邉さんが書かれている示したい命題 ∀x↑∈R^{3} rotE↑(x↑)=0⇒∀x↑∈R^{3}∃(φ)：E↑(x↑)=-grad φ(x↑」の右辺は，ちょっと違うのではないかと思います．これだと，x↑によって関数φが異なってもかまわないことになります． ∃(φ)∀x↑∈R^{3}：E↑(x↑)=-grad φ(x↑) とするのが正しいと思います．従って対偶は ∀(φ)∃x↑∈R^{3}：E↑(x↑)≠-grad φ(x↑)⇒∃x↑∈R^{3} rot E↑(x↑)≠0 」になると思います．いずれにしても，対偶を証明するよりは，積分を用いて直接φを構成するほうが簡単だと思います．

Re: 静電ポテンシャル

渡邉さんのレス (2005/12/26(Mon) 18:12)

修正，ありがとうございます．

＞いずれにしても，対偶を証明するよりは，積分を用いて直接φを構成するほうが簡単だと思います．

全くその通りだと思います．そのような考えに至るまでに，このような事を考えてみる時間が僕には必要でした．積分を用いた証明は，大学での力学の時間から見たり，書いたりする事はありましたが，あまり分かっていなかったと思います．（はじめ証明した事ないと書きましたが，した事ありました．1年の頃にやった事は，もう一度考え直す必要がありそうです）

[home] [掲示板] [ページの先頭]