最大振幅をこえる確率

蛍さんの書込 (2005/12/05(Mon) 23:20)

こんばんは，大学1年で，高校で物理未履修の蛍です．

量子力学的調和振動子では，古典論的調和振動子の最大振幅（Ａとする）を超えたところでも，波動関数Ψは０でない値を持っている．量子力学的調和振動子のｎ＝０の場合において，振幅がＡを超える確率は何％か

このようなレポート問題を解いていますが，これに関する事項に授業では全く触れていません（レポート問題は院生が作るため）．それで，教科書を見てもどこを参考にしていいのか，そもそもほとんど知識がないため手がついていません．途方にくれています．

何か解き方や，この問題にかかわる重要事項のアドバイスをいただけないでしょうか．よろしくお願いします．

古典論的調和振動子のエネルギーをm，ω，A を用いて表したものを，基底状態のエネルギー 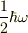$\frac{1}{2}\hbar\omega$ に等しいとおけば，振幅Aが求まります．そのAと，基底状態の波動関数を用いれば，Aを超える確率が計算できます．

ありがとうございます．波動関数の二乗をAから無限大まで積分して，約7.9％という答えが出ましたがこれでいいのでしょうか？

振動は平衡点の両側にまたがって行われるので，その値を２倍する必要があります．

わかりました．ありがとうございました．