惑星の運動
惑星の運動
カイ さんの書込 (2005/12/01(Thu) 14:04)
こんにちは．問題でわからないことがあったので質問させてください．
質量ｍの物体が逆二乗の中心力（ｒの関数）をうけて，長半径aの楕円軌道を描いて運動している．この物体の速さをｒの関数であらわせ．
自分の回答
極座標で運動方程式を記述すると
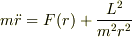だからエネルギー保存則はE=k/2aであることから（ｋ＞０です）
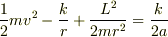となる．あとはｖについて解く．
ここまではできたのですが，初期条件が問題にないのでどうしても角運動量Lの項
がきえません．その項が０になれば，答えと一致するのですが・・・．
Re: 惑星の運動
山旅人 さんのレス (2005/12/01(Thu) 18:34)
初めまして，山旅人と申します． 単なる書き間違いかもしれませんが，第１式右辺第２項分母の ｒ の次数は ３ （Ｌ 2 /ｍ 2 ｒ <b>3</b> ） です．
> エネルギー保存則は E=k/2a であることから
ここ，私には ？？ です． 角運動量の項は消えなくてもいいのではありませんか．
テキストはお持ちのことと思いますが，以下のサイトが大いに参考になると思います．じっくりお読みください．
Re: 惑星の運動
カイ さんのレス (2005/12/01(Thu) 19:31)
次数の件は打ち間違いでした．すみません． ＞> エネルギー保存則は E=k/2a であることから ここ，私には ？？ です． 角運動量の項は消えなくてもいいのではありませんか．
「エネルギー保存則」を「力学的エネルギーEは」に訂正です．Eの式は教科書にa=k/2Eという式が書いてあったので利用しました． 答えは結果しかないのですが， ｖ^2＝k/m(2/r - 1/a)と書いてありました．Lが０になれば一致しますよね？
Re: 惑星の運動
山旅人 さんのレス (2005/12/01(Thu) 22:29)
> Eの式は教科書にa=k/2Eという式が書いてあったので利用しました． > Lが０になれば一致しますよね？ ここが安易なのではないでしょうか．こんな単純なことではないことは，教科書もしくは上記サイトを精読されればおわかりになると思います．
Re: 惑星の運動
カイ さんのレス (2005/12/01(Thu) 23:37)
a=l/1-ε^2にlとεの定義式を代入すればk/2Eになるのはわかったのですが， それでも角運動量の項が邪魔で一致しません．ヒントをくれませんでしょうか？
Re: 惑星の運動
yama さんのレス (2005/12/02(Fri) 00:33)
エネルギーの保存を表す式が間違っています． 動径方向の運動方程式に角運動量Lが出てくるのはdφ/dtを消去したためです． しかし，エネルギーの保存を表す式のvは動径方向だけでなく角度方向の速度成分も含んだ速さです．つまりdφ/dtも含まれています． dφ/dtが消去されているわけではないので，エネルギーの保存を表す式にはLは現れません． つまり，あなたの書かれたエネルギー保存の式で，Lを含む項は初めから不要です．
Re: 惑星の運動
カイ さんのレス (2005/12/02(Fri) 01:04)
それでは僕が求めてしまったのは，動径方向のみの速さということでしょうか？ エネルギーになるとスカラーになってしまうので気付かなかったのですが，ベクトルｒについて考えなければいけなかったということですね．
