合流型超幾何関数…の入り口で詰まっています

合流型超幾何関数…の入り口で詰まっています

dawn さんの書込 (2005/11/09(Wed) 18:34)

はじめまして．大学で物理を学んでいるdawnと申します．もう３回生になるのですが，未だに基本的な知識の不足からか問題を解いていて妙な所で引っかかってしまいます．今回このページをみつけて，皆様のお知恵を借りたいと思った次第です．

現在悩んでいるのは，量子力学に関連した，合流型超幾何関数…の入り口の所です．レポートの問題になったので教科書を読んでみたのですが，よくわからない箇所があるのです．

合流型超幾何微分方程式

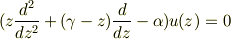
(z\frac{d^{2}}{dz^{2}}+(\gamma-z)\frac{d}{dz}-\alpha)u(z)=0

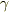（ \alpha :定数， \gamma ：０や負の整数ではない）でｚが０のまわりにあるとき，上式は

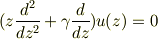
(z\frac{d^{2}}{dz^{2}}+\gamma\frac{d}{dz})u(z)=0

となる，という記述が教科書にあったのですが，ｚ〜０でγ−ｚ〜γとなるのは納得できても第三項が消えてしまうのは納得できません． 教科書には当たり前の事のように書いてあるので何か単純な事を見落としているのだと思うのですが…． 使っている教科書は，猪木慶治・川合光著の量子力学です．

それでは，よろしくおねがいします．

Re: 合流型超幾何関数…の入り口で詰まっています

渡邉 さんのレス (2005/11/09(Wed) 21:03)

どうもはじめまして．僕も3回生です．しかも合流型なんて，使った事ないです． が，これくらいなら分かりそうです．オーダー解析ってのを流体力学で去年聞いたときに「d/dz〜O(z^{-1})として良い．」という話を聞いた事があります．

これを使うと (zd^{2}/dz^{2}+γd/dz)u〜O(z^{-1}u) (zd/dz+α)u〜O(u) z〜0のときは，O(z^{-1}u)>>O(u)ですね．この理由で無視してゼロと置いてokなんですよ．（オーダー解析の裏付けは，uを冪級数展開してみたら分かるんじゃないかと思います．）

・・・・

合流型の部分読んでみました．（ついでに直交関数系も） なるほど，便利ですね．F(・;・;・)の";"が奇妙なので今まで敬遠してました．

Re: 合流型超幾何関数…の入り口で詰まっています

dawn さんのレス (2005/11/10(Thu) 00:06)

渡邉さん，早速のお答えありがとうございます．確かに，これを使うとできそうです．

ところで，「d/dz〜O(z^{-1})として良い．」との事ですが，この関係が成り立つ条件というのはどのようなものなのでしょうか？冪級数展開してみましたが，どうもどんなu に対しても成り立つわけではなさそうです．例えば，u が定数や指数関数の時には成り立ちませんよね？

もしもここで説明されるのが面倒でしたら，おすすめの教科書（渡邉さんが昨年の流体力学で使ったものなど）を教えていただくのでも構いません．

それでは．

Re: 合流型超幾何関数…の入り口で詰まっています

渡邉 さんのレス (2005/11/10(Thu) 07:04)

＞どうもどんなu に対しても成り立つわけではなさそうです

ばれましたか．純粋に数学的に正しく答えるのならば，留数計算で計算する必要があるんじゃないですか．（ゼロ付近と遠方の解との解析接続を考えるときも本当は，そういう計算をする必要があるんだと思います）

僕もした事無い計算なので，何とも言えませんが．

あと，流体力学で，テキストは使っていませんでした．

・・・ その後 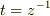t=z^{-1} で遠方の解を検討してみました．(すなわちz〜０まわりの漸近解)

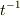t^{-1} の項を落とした後，変数を z 表示に戻すと，正しい結果が得られました．

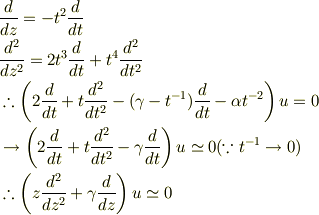
&\frac{d}{dz} = -t^{2}\frac{d}{dt}\\&\frac{d^{2}}{dz^{2}}=2t^{3}\frac{d}{dt}+t^{4}\frac{d^{2}}{dt^{2}}\\&\therefore \left(2\frac{d}{dt}+t\frac{d^{2}}{dt^{2}}-(\gamma -t^{-1})\frac{d}{dt}-\alpha t^{-2} \right)u =0\\&\to \left(2\frac{d}{dt}+t\frac{d^{2}}{dt^{2}}-\gamma \frac{d}{dt} \right)u \simeq 0 (\because t^{-1}\to 0)\\&\therefore \left(z\frac{d^{2}}{dz^{2}}+\gamma\frac{d}{dz}\right)u\simeq 0

これならば，zが遠方で効いてくる漸近解と同じくらいの精度の近似になるんじゃないですか？

Re: 合流型超幾何関数…の入り口で詰まっています

dawn さんのレス (2005/11/11(Fri) 01:37)

どうも，丁寧な説明ありがとうございます． おかげで疑問も氷解し，無事レポートも提出する事ができました．

渡邉さん，ありがとうございました．

Re: 合流型超幾何関数…の入り口で詰まっています

渡邉 さんのレス (2005/11/11(Fri) 09:59)

僕もこれを機会に，合流型幾何関数に触れる事ができて良かったです．