石井 さんの書込 (2005/11/09(Wed) 17:35)

こんにちは，石井です．こちらのようないいサイトとめぐり合うのはそう人生でも多くないと思いますので，恥を捨てどんどん教えを乞いたいと思います．

「gradのrotが0であること」と，「rotのdivが0であること」についておうかがいします．

どちらも物理数学の本とかを参考にしながら計算は追えるのですが，イメージがわきません．つまり正しく意味を理解していないのだと思います．以下の琉球大学の先生のサイトも参考にしているのですが私の理解はいまいちという感じです．

• http://homepage3.nifty.com/iromono/PhysTips/divrotgrad.html

「gradのrotが0であること」と，「rotのdivが0であること」を数式でなく出来るだけ自然言語で意味がわかるよう説明していただけないでしょうか．よろしくお願いいたします．やかん様の物理数学の記事

• http://www12.plala.or.jp/ksp/mathInPhys/vecFuntou1/index.html

を読んで，grad，rot，divの個々のイメージはつかんだつもりなのですが，よろしくお願いいたします．（できたら，上記琉球大学の先生のサイトのイメージも使って説明いただくと嬉しく思います，よろしくお願いいたします）

トミー さんのレス (2005/11/09(Wed) 21:05)

石井さん，はじめまして．トミーといいます．「rotのdivが0であること」について，少し長くなりますが頑張って説明を書かせていただきますので読んでくださいますか？

私はrotの話をする時には，よく「風見鶏」の回転を用います．想像してください．今，風がビュッと吹いて，風見鶏が上から見て反時計回りに回り始めたとしましょう．この時，その風見鶏の回転方向に右手でねじを回すような動きをしてみてください．すると，それはねじをゆるめる回転の向きなので，手が下から上に上がっていきますよね？腕が無限に伸び縮みするとすると，手は風見鶏の足元から頭に向かう方向に動いていきます．この手の動きを，何らかの物の動き(水の流れとか，風の流れとかのことです)とします．この物の動き(つまりベクトル)がrotです．

ここで風見鶏の中心付近に小さな立方体の格子を置いてみましょう．すると，格子の底から天井面に向かってその物が，同じ量だけ流れ込んで，同じ量だけ出て行くのがお分かりいただけますでしょうか？これがdivです．同じ量だけ出入りするのですからdivは0になります．

以上をまとめると，rotのdivは0になる，という結論が得られます．

いかがでしょうか？よくわからない部分がありましたら再度ご質問ください．ちなみに「gradのrotが0になる」はまた後日．長くなりますので分割いたしましょう！

Joh さんのレス (2005/11/09(Wed) 21:11)

トミーさんとだぶりますが，もっと簡単に説明を試みます．

divは，出たり入ったりの総量です

rotはグルグルです．

流れがグルっと一周してたら，その外部からの出入りはありません．出入りがあったら，グルっとできません．・・・・こんなイメージでどうでしょうか．

横槍ですが， さんのレス (2005/11/09(Wed) 22:00)

Johさんの説明は間違っていると思います．

Johさんの説明していることは， 「rotA≠０ならばdivA＝０」 という主張です． グルグルするのも，出たり入ったりするのもベクトルAの方で，divやrotはそれを計算したものです．

そして， 「rotA≠０ならばdivA＝０」 は間違っているのでJohさんの説明は間違っています．

また，質問者が参考にしているページから考えて，もっと詳しく正確な説明を質問者は求めていると考えます．

横槍ですが， さんのレス (2005/11/09(Wed) 22:38)

僕なりの説明をしようと思ったのですが， 参照されていたページ以上にわかりやすく説明できそうに無いのでやめます．

あのページを繰り返し繰り返し読むのが一番だと思います．

渡邉 さんのレス (2005/11/09(Wed) 22:52)

横槍さんの突っ込み自体が，本題と違いますね．divrot = 0 の説明と「rot≠0ならばdiv=0」とは話が違います．Johさんの説明のまずい所は，僕には分かりませんね．

やかん さんのレス (2005/11/10(Thu) 17:25)

＞数式でなく出来るだけ自然言語で意味がわかるよう説明していただけないでしょうか．

という事ですよね．厳密には成分で計算すればいいんでしょうけど，言語だと難しいですね． (^^; 勾配（grad）は常に一番きつい勾配の向きだから，なだらかなところが途中あったにせよ，ひたすら登りつづける．だからどこの範囲の面をとったとしても，二度と同じ所（低いところ）には戻ってこないから，ループ状にならないんで，回転の値ゼロ（ホント？！）嘘かもしれません・・・．

Joh さんのレス (2005/11/10(Thu) 17:28)

私の説明はまずかったでしょうか． 横槍さんの書かれたような議論をしたつもりはないのですが，私の書き方はあまりにいい加減だったかも知れません．私自身は，横槍さんがおしゃっているような勘違いはしておりません．数式ではなく自然言語で，というのは難しいですね．

石井 さんのレス (2005/11/10(Thu) 18:30)

トミー様，joh様，横槍様，渡邉様，やかん様，皆様ありがとうございます．私も皆様方のご意見をもとに考えてますので，活発なご意見をよろしくお願いいたします．

横槍ですが， さんのレス (2005/11/11(Fri) 00:01)

しつこいかもしれませんが，僕にはJohさんの主張はやはりちがうんじゃないかと思います． 僕が問題としているのは， >流れがグルっと一周してたら，その外部からの出入りはありません．出入りがあったら，グルっとできません． の部分です．

流れがグルッ一周というのはrotA≠０かつdivA＝０の状況であり， その外部からの出入りがないというのはdivA＝０をさすと思います． div rotA＝０の説明とはなっていません．

divもrotも０でない量を考えたとき（台風の写真のようなイメージ），Johさんの説明ではよくわからないと思います．こんなときでも常にdiv rotは０となるのでやはり違った説明をするべきだと思います．

僕は琉球大学の先生のページが極めてわかりやすいと思うので，石井さんはあのページを繰り返し呼んでみたほうがいいと思います．（ちなみに，僕は琉球大学の先生とは何の関係もありません．)

渡邊さんが >divrot = 0 の説明と「rot≠0ならばdiv=0」とは話が違います． といっていますが，だからJohさんの説明は的外れだというのが僕の主張です．

R さんのレス (2005/11/11(Fri) 01:45)

四角形abcdを描いたとき，divはそれぞれの線分の中点から線分に垂直で，外に向かった方向のベクトルのイメージで，rotはそれぞれの線分上に矢印を左回りに描いたイメージで，divgradは線分abの中点に外から垂線方向に，bcの中点に外から垂直に，cdの中点から外に向かって垂直方向に，そしてdaの中点から外に向かって垂直方向に向いたベクトルのイメージで，divrotはabを伸ばした方向のベクトルとbcを伸ばした方向のベクトルとcdを伸ばした方向のベクトルとdaを伸ばした方向のベクトルのようなイメージです．

やかん さんのレス (2005/11/11(Fri) 12:45)

とすると，

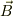は，必ずある面に垂直！と言っていいでしょうか？ （もちろん，必ずしもある面がきっかりｘｙ平面とは限らず，ｘｙ平面とｙｚ平面とｚｘ平面の間の斜めの平面かもしれませんが・・・） もしそうであれば，その図を見つつ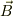， が貫く微小立方体を考え，トミーさんがご説明された風見鶏のお話のように，出納ゼロで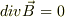， と言える！（ある面に垂直なベクトルの発散は絶対ゼロ）でしょうか・・・．既出のご意見と全く同じ事を言ってるだけかもしれませんね・・・．

石井 さんのレス (2005/11/11(Fri) 19:39)

皆様，活発なご意見ありがとうございます．皆様が活発にのべていただくので，私が「gradのrotが0，rotのdivが0であること」についてもっているイメージをいちようの為述べます．

「gradのrotが0」について， いままで持っていたイメージはrotは線積分の極限と関係しているなあと思っていて，ある点ｒのまわりの閉じた経路ｃの線積分?V dl （ Vはベクトル）はｒの回りでベクトルが経路ｃにそってまわっているかの情報を持っているから，でr点を囲むこの経路ｃの面積をΔaとすると，Δaを小さくしていけば点ｒにおけるベクトル場のまわりぐあいといえる．lim Δa→０１/Δa ?V dl =ｎ・rotV（r）となる．（ｎは軸方向単位ベクトル）すると，rot gｒadはgradの閉じた経路の線積分一周だから０だよなあといったかんじです．

「rotのdivが0であること」 についてはdivは面積分の極限と関係しているなあと思っていて，ある点ｒの湧き出しは点rを内部にもつSをとってそのSで囲む体積をΔｖとすると，面積分∫（面積分）V da は点rのまわりからどれだけ湧き出すかの情報をもっているから，Δｖを小さくしていけば点rの湧き出しをあらわす．で，div rotではrotの面積分はストークスの定理でS上でrotV（ｒ）の面積分はSの境界上のベクトルV(r)の線積分に等しくて，Sが境界をもたない閉じた面ならその線積分は０になる．よってdiv rot＝０といったイメージを持っていたんです．

上の説明は数式を使ってもっと厳密に述べるべきでしょうが，私のイメージを伝える為にある程度の数式を使って（私だけすみません）説明いたしました．（ですから私のだいたいのイメージをつかまれたら忘れてください．）

でも琉球大学の先生のサイトとかみていたら，もっと面倒でなく，直感的な理解ができないかと思って今回，「自然言語で」とお願いしました．

琉球大学の先生の説明を横槍様のおっしゃるとおり，何度か読みましたが理解してません．横槍様はじめ皆様，琉球大学の先生の説明をもっと分かりやすく（あれ以上できないといわれそうですが）説明していただけないでしょうか．（特に「gradのrotが0であること」と，「rotのdivが0であること」について） 先生の御説明は以下のサイトです．

• http://homepage3.nifty.com/iromono/PhysTips/divrotgrad.html

またトミー様はじめ皆様の個々の直感的説明もお願いいたします．