石井 さんの書込 (2005/11/07(Mon) 17:39)

こんにちは．高校生の石井です．受験の年ではありません．受験技術でなくもう少し本質を勉強しようとしていましたら，分からなくなりました．ぜひ御教授下さい．

伝送線路のホームページをみていたら，「物理的実態はマックスウェル方程式で表現される電磁界で，これが電磁波の形で線路に沿って伝わり，ポインティングベクトルで表現されるその電磁エネルギーの一部が導体内部に入り込むことによって導体に電流が流れるわけですから，電圧が原因になって電流が流れ，電圧と電流によっってエネルギーが伝送されるわけではありません．」とありました．

後藤尚久氏の「なっとくする電磁気学」等の本を読み，

・・・・・・A・・・・・・・・・ ・・ ・↓・ ∩電∩ 電気抵 池力抗 ∪線∪ ・↓・ ・・・・・・B・・・・・・・・・

上のような回路（・・は切れ目ない導線です）で，導線を電流が流れるとき，A側とB側の導線間には電気力線ができその電気力線が移動することを勉強したのですが，そこでは導線を移動する電子の移動により導線AB間に電気力線が出来ているというかんじでした．

しかし，上記の伝送理論の説明では，電池から抵抗に向けて移動する（電界）電気力線が主体で，それにより電子が動いているいう印象をうけます．

質問?導線を流れる電子の移動により電気力線が出来たと考えるべきでしょうか，それとも電界のほうが主で，それにより，電子が移動すると考えるべきでしょうか．

質問?「ポインティングベクトルで表現されるその電磁エネルギーの一部が導体内部に入り込むことによって導体に電流が流れる」というのは大変面白いのですが，もしそうなら，どのようにしてポインティングベクトルが電子の移動となっているのでしょうか．数式でも構いませんポインティングベクトルのエネルギーが電子の運動エネルギー（?)に変わっていくのかその過程を示していただけないでしょうか．

電磁波の侵入や量子力学など難解なことも関係しているかもしれませんが （S=E×Hとか電波のこととかは一般書で少しは勉強いたしました），「ここからは量子力学をしっかり勉強しないと」などと限界を示されながらでもかまいません．（分からない点があったらまた質問させていただきます）ぜひとも知りたいのです．よろしくお願いいたします．

渡邉 さんのレス (2005/11/07(Mon) 19:24)

どうもはじめまして．少しわき道にそれるような事になるかもしれませんが，良かったらお付き合いください．

連続なパラメタで特徴付けしている場の量で，電子がどう動くかを考えると混乱するのは無理もありません．例えば，天気図の風の分布を見て大気中の分子がどのように動くのか「う〜ん，わからない」と思うようなものですから．

[場の量（例として電流密度）] 電荷の分布を電荷密度という連続関数 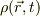で表して，電荷分布の移動度を 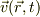で表すと電流密度は 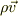です．これは電荷という物理量を持った粒子達が動き回っている際の，電荷密度の流れを表しています．このとき 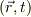という連続パラメタで名前を付けてます．（運動を追う場合は，i番目の粒子の電荷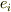を その速度を 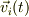などと名前を付けます．このとき名前の付け方は連続の値をとりません．）

[電流密度から電子の運動は，直接には分からない]

もしある場所で，微小領域の全電荷の50パーセントが残りとは，全く逆へ移動していたら電流はその位置ではゼロになります．これが，微小領域がゼロの極限でも成り立てば電流密度はゼロです．（実際には，粒子は行き来しているのにも関わらず）

ここまで，読まれたら分かると思いますが，個々の電子の運動が分かるのと，場の状態が分かるのとは少し違うんです．

[場の見方を身近にしてみる試み] お店をやるときに，コストと売り上げを考えるのが場の考え方．そうではなくて，お金に名前を書いてその動きをずっと追っていくのが電子の動きを追う考え方．などと言った方が分かりやすいかもしれません．

お店の人は，おつりとして払ったお金（電子）のその後には興味は無いんですよ． 利益，つまりお金の流れ（電流）に興味があるんです． （局所的にこのように考えるのは，そんなに嘘は言ってないと思います．場の量は関数なので，あらゆる場所，時間の情報が詰まっています．）

石井 さんのレス (2005/11/08(Tue) 19:30)

渡邉様おこたえありがとうございます．詳しく読ませていただき勉強いたします．この周辺のことをまた質問するかと思いますが，御教授をお願いいたします．

桝岡 さんのレス (2005/11/08(Tue) 21:41)

伝送線路は，エネルギーの伝達よりも信号（電流や電圧の変化）の伝送が目的のため，ポインティングベクトルを主体とする説明には魅力がありますが，物理的実態と言うのは無理があると思います． 信号の伝達速度は，導体の周囲の電磁場の性質により決定されますが，エネルギー自体は，導体に流れる電流により伝達されると考えたほうが，物理学上は，合理的だと思います．

質問１．電池を接続する(原因)ことで，{電界が発生し，電子が移動する}(結果)，のだと思います． 電界の発生と，電子の移動で，どちらが主なのか，見方によって違ってくると思います． 伝送線路として，信号の伝達速度を考えると，電磁界の形成速度により，電流の伝達速度が光速に制限されるので，電磁界が主と考えることもできます． 一方，物理的なエネルギーの伝送として考えると，電子の移動が主のように思えます． 電界の発生と，電子の移動は，同時と考えて良いと思いますが，あえて原因と結果に分類するなら，電界の発生が原因のように感じます．（電池を接続したのが根本原因だから）

質問２．「ポインティングベクトルで表現されるその電磁エネルギーの一部が導体内部に入り込むことによって導体に電流が流れる」というのは，物理的には間違った説明だと思います． 伝送線路の場合，伝送速度はポインティングベクトルでも説明できますが， ・信号源で，エネルギーがポインティングベクトルに変換される方法 ・負荷で，ポインティングベクトルが電流と電圧に変換される方法 ・直流を伝送できる理由 を説明できません． 導波管であれば，エネルギーはポインティングベクトルで伝達されます．信号源と負荷のところに，変換用のアンテナが付いていて，直流は伝送できません．

伝送線路について，以前にも投稿したのですが，図が使えないとわかりにくいので， 簡単な解説ページを作ってみました．

• http://www.aa.isas.ne.jp/v-tails/phy/densou.html

石井 さんのレス (2005/11/09(Wed) 17:04)

桝岡様丁寧なご返事ありがとうございます．解説ページをみて（まだじっくりとは読みきれてませんが）たいへん感激，感謝をしております．ありがとうございました．解説ページはじっくり勉強させていただき，質問もさせていただきたいと思います．ひょんなことから勉強し始めたのですが，伝送線路っておもしろいなぁと思っております．

先に引用しました「物理的実態はマックスウェル方程式で表現される電磁界で，これが電磁波の形で線路に沿って伝わり，ポインティングベクトルで表現されるその電磁エネルギーの一部が導体内部に入り込むことによって導体に電流が流れるわけですから，電圧が原因になって電流が流れ，電圧と電流によっテエネルギーが伝送されるわけではありません．」 というのは

• http://www.mogami-wire.co.jp/paper/tline/tline-01.html

という伝送線路理論の基礎というサイトの（１電信方程式）というところにあります．ホームはモガミ電線株式会社という会社だそうですが，記事を書かれている方も会社もとてつもなく熱意ある立派な方のようです． （ほとんどの記事は理解できてませんが，すごいことがかかれていそうという感じです）会社は

• http://www.mogami-wire.co.jp/ のようです．

桝岡様はじめ皆様には理解していただき，私にエッセンスだけでも御教授をお願いいたします．

これより桝岡様の解説ページを読んで考えたいと思います．（まだ上記のサイトの言葉が残っているのですが（笑い））

ぜひ，桝岡様も上記サイトをみていただき，桝岡様との考えのちがい，同じ点を浮き彫りにして，伝送のエッセンスを御教授ください．

桝岡様以外の皆様もよろしくお願いいたします．

ｙama さんのレス (2005/11/09(Wed) 17:21)

電流の発生についての桝岡さんの解説ページは，非常にわかりやすくていいですね．

桝岡さんがあまり書かれていない定常電流でのエネルギーの移動について少し書いておきます. 電流のエネルギーは，高校物理に関する限り，また大学でもほとんどの場合，電流または電子によって運ばれると考えていいでしょう．電子は負電荷を持つので，電位の低いところにある電子は大きい位置エネルギーをもち，位置エネルギーの減少する向きに力を受けて運動します．それにともなって位置エネルギーが減少し，運動エネルギーが増加します．また原子やイオンに衝突して運動エネルギーを与えます．それは巨視的に見ればジュール熱の発生になります． つまり電流のエネルギーは，電子の持つ位置エネルギーの形で運ばれるわけです．

これとは別の考え方として，電磁場がエネルギーを持っていて，電磁場と電子との相互作用によってエネルギーがやり取りされると考えることもできます．電流が流れるとき，導線や抵抗内の電磁場のエネルギーの一部が電子の運動エネルギーに変わるわけです． それだけだったら，電磁場のエネルギーが減少していくので，一定のエネルギーを保つためには何らかの形でエネルギーが供給されないといけません． 電磁場のエネルギーの流れはポインティングベクトルで表されますが，それによるとエネルギーは電池から出て空間を通って導線や抵抗に流れ込むことになります． この場合，電磁場が変動するわけではないので，電磁波が伝わっていくわけではありません．導線に沿って電磁波が伝わるわけではないので，エネルギーも導線に沿って伝わるわけではありません． 注意すべき点として，電磁場とは別にポインティングベクトルというものがあるわけではなく，電磁場があればそれにともなってポインティングベクトルが考えられるということです．ポインティングベクトルによって運ばれるエネルギーは電磁場との相互作用を通じて電子との間でやり取りされます．また，静的な電磁場においてもポインティングベクトルで表されるエネルギーの流れが存在します． このような考え方については異論もあり，ポインティングベクトルが常にエネルギーの流れを表しているわけではないという考え方もあります．

将来，電磁気学を学ぶときに，このあたりのことを念頭において学ぶと理解が深まるでしょう.

渡邉 さんのレス (2005/11/10(Thu) 13:25)

>このような考え方については異論もあり，ポインティングベクトルが常にエネルギーの流れを表しているわけではないという考え方もあります．

この考えの部分は，プランクの関係式によって決着がついたのではないですか？ ポインティングベクトル 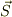電磁場の運動量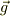

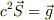
これが常に成り立つので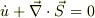， が成り立つ範囲で考えて，ポインティングベクトルに任意の循環項を入れて良い．というのは，間違っているという話です．（今回の問題の場合，外部電場が入ってくるのでこのような関係は成り立ちません．簡単に閉じた系を考えてます）

石井 さんのレス (2005/11/10(Thu) 18:34)

ｙama様，渡邉様，かなり高度なおはなしとなってまいりましたが，楽しく読ませていただいております．発展的なご意見，今後も楽しみといたします．

桝岡 さんのレス (2005/11/10(Thu) 21:43)

http://www.mogami-wire.co.jp/paper/tline/tline-01.html

を見ました． ポインティング・ベクタについて，誤解していました． ＃まだ，正確には理解できていませんが．． 前回の説明を，少し訂正します．

伝送線路の電信方程式は工学的解釈ですが， 私の印象としては，ポインティング・ベクタは物理的実態よりも，物理的解釈のように思えます．

>どのようにしてポインティングベクトルが電子の移動となっているのでしょうか．

電圧によって電界が形成され，電流によって磁界が形成されるので，電界と磁界のベクトル積であるポインティング・ベクタは，電気エネルギーの流れを意味することになります． ポインティング・ベクタが存在すれば，電界と磁界が存在するので，電界に相当する電圧と，磁界に相当する電流が，そこの導体に存在します．ポインティング・ベクタの存在と，電子の移動は，見方が違うだけで，同じ現象です． もちろん，ポインティング・ベクタの分布は，導体の電圧と電流で形成される電磁界の分布状態にしかなりません． また，ポインティング・ベクタの存在がエネルギーの流れを意味するのであって，ポインティング・ベクタが移動してエネルギーが伝達されるのでは無いと思います．

>ポインティング・ベクタ表現されるその電磁エネルギの一部が導体内部に入り込むことによって導体に電流が流れる

ポインティング・ベクタと，導体に流れる電流によるエネルギー伝送は，同じ現象を違う立場から見ているだけなので，やはり，この表現は間違っていると思います．

見方が違うだけなので，どちらが物理的実態なのか，判断は難しいですが， 電流の場合は電子，電磁波の場合は光子，という粒子の移動を伴いますが，ポインティング・ベクタの場合は対応する粒子の移動を伴わないので，伝送の本質を表現していると言えても，物理的実体とは言いにくい感じがします． #物理学としては，実体よりも，本質や数学的表現のほうを重視しそうですが．

ｙamaさんへ 電子の位置エネルギーによる，定常電流でのエネルギー移動の説明，ありがとうございます． 私の解説ページにも，定常電流について，少し追加したいと思っています．

渡邉 さんのレス (2005/11/10(Thu) 22:05)

＞ポインティング・ベクタが移動してエネルギーが伝達されるのでは無いと思います．

すみません，少し良いですか． そもそも場の量が移動するというのは，どのような状況を指しているのか分からないのですが．（HPの方にもそのような言葉がありました．いずれも否定形になっているのですが，僕はそのような用語を聞いた事がありません）

ｙama さんのレス (2005/11/11(Fri) 18:08)

ポインティングベクトルについては，渡邉さんが書かれている通りで，循環項を加える任意性はありませんね．

位置エネルギーによるエネルギー移動の説明ですが，前に書いたようにこれで一応は説明できますが，定常電流の場合にしか適用できないという点を別にしても，物理的実体という点ではあまり満足な説明ではありません． というのは，位置エネルギーは物理的な実体とは考えにくいからです．電子の位置エネルギーが変化するといっても電子自体の状態が変化するわけではありません．大きい位置エネルギーを持っていても，電子自体がなんらかの励起状態にあるわけではありません． 電磁場の中に電子がある場合に位置エネルギーを持つわけであって，電磁場と無関係に位置エネルギーを持つわけではありません． 従って電子が位置エネルギーを持つというのは，運動を説明するための多分に便宜的な考え方であって，実体的なものとは言いにくいと思います．

似た例をあげると，バネに取り付けた物体の運動があります． この運動は物体の運動エネルギーと位置エネルギーを用いて説明することができますが，位置エネルギーが大きかろうと小さかろうと物体自体の状態は変わらないので，物体の持つ位置エネルギーは物理的実体とは考えにくいでしょう．

これに対して，物体が位置エネルギーを持つのではなく，バネがエネルギーを持っていて，バネと物体の相互作用によってエネルギーがやり取りされると考えることもできます．このような見方のほうが物理的実体として受け入れやすいのではないでしょうか． これは電磁場がエネルギーを持っていて，電子との相互作用によってエネルギーがやり取りされるという考え方に相当します.

石井 さんのレス (2005/11/11(Fri) 20:27)

桝岡様，渡邉様，yama様ありがとうございます．

質問? 「ポインティングベクトルに任意の循環項を入れる」，入れないとは何のことでしょうか．高校生にも分かるよう教えていただけないでしょうか． 質問? yama様のおっしゃる「電磁場がエネルギーを持っていて，電子との相互作用によってエネルギーがやり取りされる」というとき，その相互作用ってどんな相互作用ですか． 質問? yama様の御意見では伝送線路のサイトに書かれている「ポインティングベクトルで表現されるその電磁エネルギーの一部が導体内部に入り込むことによって導体に電流が流れるわけです」といってもいいわけでしょうか． 質問? 分かりやすい伝送線路の本はないでしょうか．

ただいま考えをまとめようと桝岡様の説明ページをもとに勉強しております．今後も皆様よろしくお願いいたします．

yama さんのレス (2005/11/12(Sat) 00:20)

?について ポインティングベクトルに，任意のベクトルの回転を付け加えることです． これをエネルギーの流れの密度としても，回転の発散が0になるために，エネルギーの保存の式は成り立ちます． このためエネルギーの流れの密度が一意的に定まらなくなります． しかしこの場合，エネルギーの流れの密度と運動量の間に正しい関係が成り立たなくなります．

?について 相互作用とは，電磁場が電子に力を及ぼしたり，逆に電子がつくる電磁場によって電磁場が変化することです．

?について ポインティングベクトルで表されるエネルギーの流れがあるとは言えますが，それが電流が流れる原因になっているかどうかは微妙なところです． 電流にともなってエネルギーの流れが生じているようにも思えます．

?について 伝送線路は工学的な概念なので，工学系統の本にのっていると思いますが，具体的な書名は私にはわかりません． 物理系統の電磁気学の本には，全くのっていないか，のっていてもあまり詳しくはないようです．

石井 さんのレス (2005/11/12(Sat) 09:08)

yama様ありがとうございます．「なるほど」という話ばかりです．

また今後もよろしくお願いします．