電磁気

home > 掲示板 >

このページのPDF版

サイトマップ

電磁気

あさ（高校で物理やってない大学１年生☆）さんの書込 (2005/10/26(Wed) 19:50)

お久しぶりです．今度は電磁気やることになって，最近高校の教科書ひっくり返しているのですが，わからないところがあったので教えてください<m(__)m>

「アルミポットのようなへこんだ部分を持つ導体に電荷を与えられたとき，導体のどこも一定の電位となるように電荷が分布する．その結果，電荷は内壁には存在せず，全て外側の表面に分布する．」

どうして内壁には存在せず，外側にだけ存在するのですか？

Re: 電磁気

篠原さんのレス (2005/10/26(Wed) 21:33)

あささん，はじめまして（かな？）篠原です．

イメージを持っていただけるよう，定性的にご説明いたします．

（１）金属の導電率は非常に高い（２）もし，金属内部に電場が発生すると，導電率が高いためにその電場により金属内部の電荷が移動する．（３）その結果，金属内部では電場は０となる．（４）電場が０となるため，ガウスの法則により，金属内部には電荷は分布しない．（５）もし，金属外部に電場が存在すると，金属表面を含む体積においてガウスの法則を適用すると，金属表面には電荷が分布することになる．

以上のことから，記述のとおり，「電荷は内壁には存在せず，全て外側の表面に分布する．」ということが説明されます．

＊ガウスの法則について＊なお，ガウスの法則は，噛み砕いて述べると，「電場が変化する場所に電荷が分布する」というものです．つまり，「金属内部で電場がすべて0（一定値）」ということは，金属内部では電場は変化していないため，電荷は分布していないことになります．また，金属外部に電場が存在した場合，金属内部と外部を考えると，ちょうどその界面で電場が変化しているため，その界面に電場が分布していると考えられるのです．

篠原さんへ（たぶん以前もお世話になった気がします<m(__)m>）

あさ（高校で物理やってない大学１年生☆）さんのレス (2005/10/27(Thu) 01:44)

お返事いただけてありがたかったので，とりあえずお礼の返信だけ今しておきます（内容については時間が時間なのでまた明日考えます．．．．＠am1:40）

ただぱっと見，ポットの内側にはなくて外側には電荷がある，ということに，お返事のどこが対応しているのかよく分からなかったので，そこらへんをもう一度詳しく説明していただけるとありがたいです．．．ここでの話は金属（板）の表面の内部の話をしているのではなく，アルミポットの断面図を書いたときに，外側には電荷があって内側には全くないという状況です．反対の電荷をもった金属球の振り子を近づけるとぽっとの内側では無反応で外側では球がポットに引き寄せられるっていう話です．

私が誤解していたらごめんなさい．よろしくお願いいたします．．．

Re: 篠原さんへ（たぶん以前もお世話になった気がします<m(__)m>）

篠原さんのレス (2005/10/27(Thu) 14:04)

あささん，すみません．少し問題を間違ってとらえていたようです．

この問題の場合，「電荷は内壁には存在せず，全て外側の表面に分布する．」ということが，成立するには，「ポットの中には電荷が存在しない」という条件が必要になります．

ポッドの中に電荷が存在しない場合，ガウスの法則によりポッドの中では電場はすべて０になります．

一方，金属内においても，電場が0であるため，ポッド内壁を含む体積においてガウスの法則を適用した場合，ポッド内壁には電荷が分布していないという結果が得られます．

Re: 篠原さんへ（たぶん以前もお世話になった気がします<m(__)m>）

渡邉さんのレス (2005/10/28(Fri) 13:36)

面白い問題ですね．僕も考えてみました．ポイントだけ書きますと 1.導体中はオームの法則に従う →静電場では，電流がゼロなので導体中の電場はゼロになっている

2.ガウスの法則の積分形（任意の閉曲面の外にある電荷は電場に影響しない．逆に内側のは電荷として数える）

1.と2.を合わせれば，電荷は内側には電荷は存在できません．もし電荷があるとすれば，2.より導体中に電場が存在する事になります．すると1.より電流が流れるというわけです．これが流れ続けると，第一種永久機関を作る事ができます．(ジュール熱が永久に湧き出す)これは明らかに矛盾ですね．

後，基本的に電荷は導体の表面へ誘起する．この事も定量的に計算できます．

アンペール・マクスェルの法則のdivをとって，そこにガウスの法則を代入します．結果，電荷の保存則

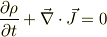
$\frac{\partial \rho}{\partial t} +\vec{\nabla} \cdot \vec{J}=0$

を得ます．導体内では，オームの法則 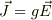$\vec{J} = g \vec{E}$ に従うので，それを上に代入します．すると電荷の時間発展方程式を得ることができます．

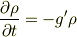
$\frac{\partial \rho}{\partial t} = -g^{\prime} \rho$

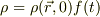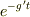変数分離( $\rho = \rho(\vec{r},0)f(t)$ )すればfの解は $e^{-g^{\prime} t}$ ．従って，導体内の電荷は 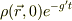$\rho(\vec{r},0)e^{-g^{\prime} t}$ に従う事が分かります．

これよりずっと長い時間の後の静電場になったとき，導体内の電荷はゼロになる事は分かるかと思います．電荷は保存するのに，導体内には電荷は無い．だったら電荷はどこに分布するのか．それは導体表面しかありません．（導体表面はオームの法則には従わない）

導体表面に一様に電荷が分布するのも，少し考えれば分かります．それは，導体表面が等電位面になっているからです．もし等電位面でなければ，境界面に平行な力が働きます．（これでは静的な状況とは言えません）

いやぁ，長くなってしまいました．すみません

[home] [掲示板] [ページの先頭]