グリーンの公式(流力から)
グリーンの公式(流力から)
taka さんの書込 (2005/10/21(Fri) 01:31)
お世話になってます.takaです.二回目の投稿です.流体力学の本(今井功,流体力学)を読んでいて出てきた,グリーンの公式について質問です.
本には,
閉曲面  の内部の領域
の内部の領域  で
で 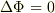 を満たす関数
を満たす関数 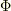 について,
について,
![\Phi (P) = \frac{1}{4 \pi} \int_{S} \left[ - \frac{1}{r} \frac{\partial \Phi}{\partial n} + \Phi \frac{\partial}{\partial n} \left( \frac{1}{r} \right) \right] dS](http://hooktail.maxwell.jp/bbslog/924043ee10678a6f57212b7e363272a6.png)
なるグリーンの公式が成り立つ.
ここで 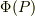 は
は  の任意の点
の任意の点 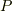 における
における 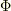 の値,
の値,  は積分点と
は積分点と 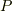 との距離,
との距離, 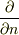 は内向き法線方向の積分とする.
と書かれていました.
でも,この公式がどうやって出てきたかが分かりませんでした.
は内向き法線方向の積分とする.
と書かれていました.
でも,この公式がどうやって出てきたかが分かりませんでした.
できれば自分で調べて,導くまでできた方のグリーンの公式,
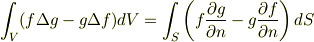
を使って上の式に変形したいです. 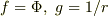 と置けば,一番上の式の右辺になり,また
と置けば,一番上の式の右辺になり,また 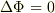 より,
左辺第二項が消えることまでは分かりました.あとは,
より,
左辺第二項が消えることまでは分かりました.あとは,
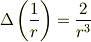
より,
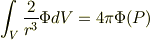
となることを導けば良いと思いますが,これからどうすれば良いか分かりません.(それに本当にこうなるか,疑問です.僕の計算間違いかもしれませんが....) ご教授お願いします.m(_ _)m
Re: グリーンの公式(流力から)
yama さんのレス (2005/10/21(Fri) 13:31)
計算が間違っています. r≠0 のとき Δ(1/r)=0 です. 従ってPを含む任意の領域の積分値は同じになります. Pを中心とする無限小の球を考えると,内部ではΦは定数(Φ(P))とみなせます. ガウスの定理を適用して球面内の積分を球面上の積分に変換して計算すると求める結果が得られます.
なお,ディラックのδ関数を用いると Δ(1/r)=-4πδ(x)δ(y)δ(z) と表すことができます.ただし,(x,y,z)は P を原点とする座標です.
Re: グリーンの公式(流力から)
taka さんのレス (2005/10/22(Sat) 02:16)
球座標のラプラシアンなので, 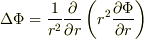 を使えば,
を使えば,
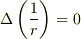 ですが,このとき
ですが,このとき  は原点からの距離ではなく,
は原点からの距離ではなく,  の任意の点なので上の計算ではなく直交座標に直してやって見ました.
の任意の点なので上の計算ではなく直交座標に直してやって見ました.
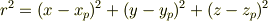
(ただし 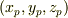 は点
は点 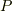 の座標)より,
の座標)より,
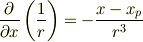
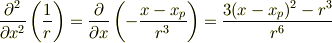
よって,
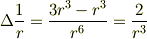
になると思います.でも,ここで 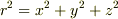 と置いても同じ結果になるため,どこかで計算間違いをしているかもしれません.どなたか計算間違いに気づきましたら,突っ込みを下さい.
と置いても同じ結果になるため,どこかで計算間違いをしているかもしれません.どなたか計算間違いに気づきましたら,突っ込みを下さい.
yamaさんのおっしゃってることは,
もし, 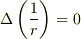 なら,
なら,
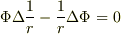 となり,(形式的に?)
となり,(形式的に?)
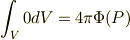
という計算をするということでしょうか?
自分でも(ごまかしごまかし)計算をしてみたのですが,本などで読んだ方法ではないので自信がないです.
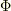 がどんな関数でも上式の左辺の値は一定なので,積分領域は
がどんな関数でも上式の左辺の値は一定なので,積分領域は 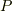 を含むなら任意になる.点
を含むなら任意になる.点 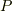 を含む無限小の球を考え,内部を
を含む無限小の球を考え,内部を 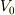 ,それを覆う閉曲面を
,それを覆う閉曲面を 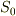 とおきます.ここで,
とおきます.ここで,
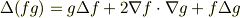
より,
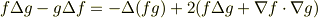
が成り立つことを利用して,
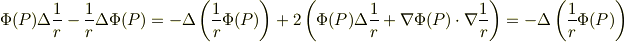
(ここで, 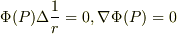 を使った.)
となります.
を使った.)
となります.
よって,ガウスの定理を使い,
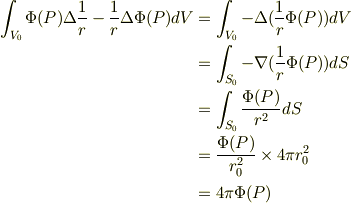
(ただし, 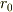 は無限小球の半径.)
となる.
は無限小球の半径.)
となる.
...という流れです.間違いがありましたら突っ込みください.また,どなたか(正しい?)方法を知ってましたら教えてください.m(_ _)m
Re: グリーンの公式(流力から)
渡邉 さんのレス (2005/10/22(Sat) 07:54)
takaさん,はじめまして.はじめのラプラシアンの定義が間違っているようです. 正しいのは
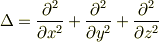
で,これは球面座標で計算した結果と同じく点Pを除いてゼロになります. takaさんの書かれている4番目の式をy,zについても書けばすぐに分かると思います.
Re: グリーンの公式(流力から)
yama さんのレス (2005/10/22(Sat) 09:35)
ラプラシアンの計算については渡邉さんが書かれている通りです. それから私が書いた「Pを中心とする無限小の球を考えると,内部ではΦは定数(Φ(P))とみなせます.」というのはあまり正確な表現ではありません. 正確には,球の半径を十分小さくすれば任意のε>0に対して|Φ−Φ(P)|<ε になるということです. 従って積分の計算ではΦを定数とみなせますが,微分するときは定数とはみなせません.つまり▽Φ=0 とおくことはできません.
Re: グリーンの公式(流力から)
taka さんのレス (2005/10/22(Sat) 12:40)
渡邉さん,yamaさん,ありがとうございます.
僕の書いた五番目の式は,
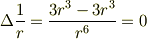
で,分子の第二項は 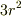 ですね.何故こんな間違いをしたのか,自分でも分かりません....投稿を削除したい(笑).
ですね.何故こんな間違いをしたのか,自分でも分かりません....投稿を削除したい(笑).
ガウスの定理による変形は...もう少し考えてみます. 手元にあるベクトル解析の本には載っていなかったので,今日は図書館に行ってベクトル解析の本を漁ってみます.