無題

無題

にしかわ さんの書込 (2005/10/11(Tue) 16:02)

初めまして，私工学系の大学院に通っている，「にしかわ」と申します． 以前，下のほうにレスをつけさせていただいたこともあるのですが，以後よろしくお願いします．一応物理の方は，工学部ということもあり，正直解析力学などは講義でやるはずもなく，独学で高橋先生の「量子力学のための解析力学」を読んで勉強している程度の「物理の基礎レベル」（専門の講義では原島鮮先生の「力学」をやりましたが）しかもっておりません．現在量子工学を専攻しており，半導体の物理（GaAsの電気伝導の実験をしています）系の研究室に所属するＭ２の学生です．

固体物理を勉強していた頃，グリーン関数の摂動論に関して記述してある本（基礎固体電子論：西村久著）を他の本も参考にしながらなんとか一冊読みきったつもりのですが，やはりグリーン関数がどのように半導体の物性と絡んでくるのかがよく分りません．結果的に計算ばかりおってしまい，その式の与える物理イメージをよく理解できなかったというか，むしろ物理イメージがわくほどの素養が身についておらず，勉強不足この上ないといった感じです．

グリーン関数についてですが，偏微分方程式を勉強している時には，その偏微分方程式の形により与えられる，０次グリーン関数を源泉，境界条件，初期条件を加味して積分することで，解が簡単に得られる，もしくはその系の物理が明確に表わせる式が得られるというのは勉強しました．

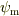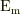しかしながら，グリーン関数は系の状態密度と密接に結びついているということは 多少理解しているつもりです．つまり，ハミルトニアン|8419bc13f0b74f6c7643c0052e3846fe|で記述される系を考えた時に規格化された固有関数を \mathrm{\psi _m} ，固有値を \mathrm{E_m} とした時に，系の状態密度は，

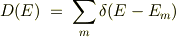
D(E) \; = \; \sum_m \delta (E-E_m)

で定義され，一方，演算子 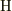\mathrm{H} の遅延グリーン関数は

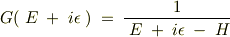
G(\; E\; +\; i\epsilon \; )\; = \; \frac{1}{\; E\; +\; i\epsilon \; - \; H}

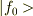\mathrm{\epsilon } は正の実数．さらにこれの対角成分は， |f_0> を規格化された状態として

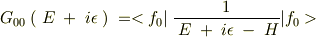
G _{00}\;(\; E\; +\; i\epsilon \; )\; = <f_0|\; \frac{1}{\; E\; +\; i\epsilon \; - \; H}|f_0>

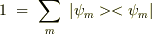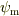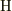を考えると，単位演算子 1 \; = \; \sum _m\;|\psi _m><\psi _m| ( \mathrm{\psi _m} は \mathrm{H} の固有関数)を挿入して，

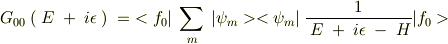
G _{00}\;(\; E\; +\; i\epsilon \; )\; =\;<f_0|\; \sum _m\;|\psi _m><\psi _m|\; \frac{1}{\; E\; +\; i\epsilon \; - \; H}|f_0>
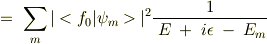
\; =\;\sum_m|<f_0|\psi _m>|^2 \frac{1}{\; E\; +\; i\epsilon \; - \; E_m}
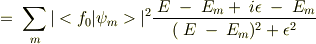
\; =\;\sum_m|<f_0|\psi _m>|^2 \frac{\; E\;- \; E_m +\; i\epsilon \; - \; E_m}{(\; E\;- \; E_m)^2 + \epsilon ^2}

これの虚部にδ関数の公式を使って，結局状態密度の表式と一致して，

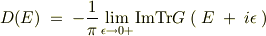
D(E) \; = \; -\frac{1}{\pi } \lim_{\epsilon \rightarrow 0+} \mathrm{Im Tr }G\;(\; E\; +\; i\epsilon \; )

となるということで，一応式をはしょって書かせていただきましたが，対角成分以外の部分や，摂動論の１次以上の高次の成分は実際の物理系にはどのような影響があるのでしょうか？グリーン関数の物理的な意味についてお教えいただければ幸いです．

かなり，長々と書いてしまったため，支離滅裂になってしまった感があって大変恐縮なのですがよろしくお願いします．

Re: 無題

渡邉 さんのレス (2005/10/15(Sat) 16:49)

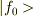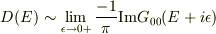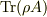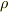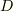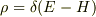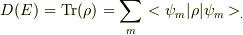どうもはじめまして．最後から二番目までの式と最後の式とのつながりがちょっと分かりません．もしかして |f_{0}> がゼロ次の摂動状態という事で1次以降の項が省略できる場合つまり D(E)\sim \lim_{\epsilon \to 0+} \frac{-1}{\pi} \mathrm{Im} G_{00}(E+i\epsilon) を考えているのでしょうか． 古典論における物理量Aは，量子論では物理量の期待値に置き換えられるという事からアンサンブル平均は \mathrm{Tr}(\rho A) になります．これと同じ理由でトレースをとるのだと思います．今回の場合は， \rho の期待値がすなわち D だから( \rho = \delta (E - H) ) D(E) = \mathrm{Tr}(\rho)=\sum_{m}<\psi_{m}|\rho |\psi_{m}>_{.} 最後の式は

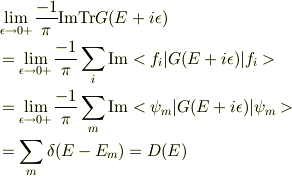
&\lim_{\epsilon \to 0+} \frac{-1}{\pi} \mathrm{Im} \mathrm{Tr} G(E+i\epsilon) \\&=\lim_{\epsilon \to 0+} \frac{-1}{\pi} \sum_{i} \mathrm{Im} <f_{i}| G(E+i\epsilon) |f_{i}> \\&=\lim_{\epsilon \to 0+} \frac{-1}{\pi} \sum_{m} \mathrm{Im} <\psi_{m}| G(E+i\epsilon) |\psi_{m}>\\&=\sum_{m} \delta (E-E_{m})=D(E)

で，トレースが基底に依らない事から理解できます．2段目と4段目に注目すると，ゼロ次が主要項になる場合，はじめに僕が書いた式が得られます． 対角成分以外という発想はどこから出るか分からないですが，１次以降の摂動解を切り捨てるのはゼロ次が主要項であるという理由に尽きると思います．