無題
無題
ACタイガー さんの書込 (2005/10/06(Thu) 12:24)
はじめまして．ACタイガーと申します．では質問させていただきます． シュプリンガーのスーパーラーニングシリーズの「力学」という本のp200ページに書いてある「半径a,密度pの球の中心軸の周りの慣性モーメント」の数式処理が納得いきませんん．sinの2乗の0からπまでの積分の計算が変です．自分が計算するとπ/2になるのですが．本書の結果は慣性モーメントが2/5Ma^2（Mは全質量）．回転半径が(2/5)^(1/2)aとなってました．若し持ってる方がいらっしゃいましたらお答え願います．
球の慣性モーメント
山旅人 さんのレス (2005/10/06(Thu) 13:53)
当該書籍は手許にないのですが…
Ｉ＝∫ρ（ｘ 2 ＋ｙ 2 ）ｄＶ ＝ρ∫ｒ 2 ｓｉｎ 2 θ・ｒ 2 ｓｉｎθｄｒｄθｄφ ＝ρ∫ 0 a ｒ 4 ｄｒ∫ 0 π ｓｉｎ 3 θｄθ∫ 0 2π ｄφ ＝ρ（ａ 5 /５）・４/３・２π ＝Ｍ/（４πａ 3 /３）・（８πａ 5 /１５） ＝<b>２Ｍａ 2 /５</b>
> sinの2乗の0からπまでの積分の計算が変…
ｄＶ＝ｒ 2 <b>ｓｉｎθ</b>ｄｒｄθｄφを勘違いされましたか？
Re: 球の慣性モーメント
ACタイガー さんのレス (2005/10/06(Thu) 17:09)
どうもありがとうございます． ところでこのサイトで数式を書くにはどうしたらいいのですか？
Re: 球の慣性モーメント
ACタイガー さんのレス (2005/10/06(Thu) 17:11)
あとここの管理人さんはどなたですか？
Re: 球の慣性モーメント
tomo さんのレス (2005/10/06(Thu) 20:32)
ACタイガーさん，こんばんは． tomoです．
> このサイトで数式を書くにはどうしたらいいのですか？
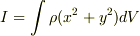のような数式を書きたいのであれば，
上付き（x 2 ）や，下付き（A 1 ）でしたら，
Re: 球の慣性モーメント
崎間 さんのレス (2005/10/06(Thu) 23:55)
> あとここの管理人さんはどなたですか？
管理は物理のかぎプロジェクトで行っています．TeX数式関係の改造を加えたり，掲示板プログラムそのものを管理しているのは COさん です．
