わかりません
わかりません
さい さんの書込 (2005/10/01(Sat) 12:35)
はじめまして．大学2年のものです． 電気は高校以来でよくわからないので質問します．
２つに枝分かれした直流回路で枝分かれした２つの導線に それぞれ抵抗ｒ１，ｒ２がある．またそれぞれに電流I１，I２ が流れている． 枝分かれする前の電流はIである． I１+I２=Iの下で発熱量を最小にする電流の分流を求めなさい． という問題なんですが 発熱量がｒ１*I１^２+ｒ２*I２^２ということまでわかったのですが 最小の求め方がわかりません． お願いします．
Re: わかりません
CO さんのレス (2005/10/01(Sat) 12:56)
,
は定数．
発熱量を 
とすると
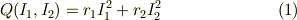
となるのですよね．また，条件として
( 
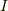は定数)が与えられています．(2)式を(1)式に代入すれば は一変数関数になります．一変数関数ならば(微分とかして)最小値が求まりませんか？
Re: わかりません
山旅人 さんのレス (2005/10/01(Sat) 13:43)
枝分かれした Ｉ 1 ，Ｉ 2 は再び合流して Ｉ になると考えてよいのですね．すると ｒ 1 ，ｒ 2 は並列に接続されていることになり， ｒ 1 Ｉ 1 ＝ｒ 2 Ｉ 2 が成り立ち， Ｉ 1 ＝ｒ 2 Ｉ/（ｒ 1 ＋ｒ 2 ）， Ｉ 2 ＝ｒ 1 Ｉ/（ｒ 1 ＋ｒ 2 ） となります．
すなわち，発熱量を云々する前に Ｉ 1 ，Ｉ 2 は決定されてしまうのです． この問題が 「 ｒ 1 ＋ｒ 2 ＝Ｒ （一定） のとき，発熱量を最小にする ｒ 1 と ｒ 2 の比を求めよ」 という問題なら 《最小》 が生きてきます．
Re: わかりません
yama さんのレス (2005/10/01(Sat) 14:02)
これは「最小発熱の原理」に関する問題だと思います． 最小発熱の原理とは，全体の電流が一定という条件の下で発熱が最小になるような電流分布が，実際の電流分布になるということです． つまり r 1 I 1 ＝r 2 I 2 を前提としないで，発熱が最小となるような電流分布を求めると r 1 I 1 ＝r 2 I 2 が導かれるというわけです． 初めから実際の電流分布を考えると，問題の意味がわからなくなってしまいますから，問題文の表現もその点がはっきり分かるように書いてもらいたいものですね．
なお，最小発熱の原理は，電気伝導度が一様でない物体中の電流分布にも適用できます．
Re: わかりません
山旅人 さんのレス (2005/10/01(Sat) 15:19)
>> yama さん いつも有り難うございます． そうなのですか．私の書き込みは，全くそっぽを向いていましたね．（滝汗！）
>> さい さん 私の記述は気にせずに無視してください．最小値は CO さんがお書きのように微分で求まりますし，２次式なので平方完成でも求まります．
