斜面上の物体の運動
斜面上の物体の運動
リク さんの書込 (2005/09/26(Mon) 18:50)
初めまして,リクと言います.高校生です.
宿題のプリントで出され自分なりに解いてみましたが,合っているのか微妙なので,間違いがありましたら,指摘お願いします.
長さ2m,高さ0.2mの滑らかな斜面がある.下端から初速0.98m/sで,斜面にそって上向きに滑らせた物体は,どこまで上がることができるか.
a = g sinθより,a = 0.98m/s
"どこまで上がれるか?"というのを"最高地点は?"と解釈して,変位x = 0とし, x = vt + 1/2at^2に代入していくと t = 0 ,0.49 となります.
0は何も力を加えてない状態なので,不適で,答えは0.49となりました. でもこれだと,重力の事は全然考えてないし,時間が0.49なので変位が求まってないという気がします.
最初から間違っているのでしょうか? どなたか,お願いします.
Re: 斜面上の物体の運動
渡邉 さんのレス (2005/09/26(Mon) 19:48)
上の解答は,なんだか違うようです.
この問題は"なめらかな"がキーワードです.つまりこのときエネルギーは保存します( 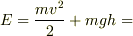 一定).だから運動方程式を解かなくても,問われた事について答える事ができます.
一定).だから運動方程式を解かなくても,問われた事について答える事ができます.
まずはじめポテンシャルはゼロで,運動エネルギーのみ存在します. (というより,ポテンシャルの基準点をそのようにとったと考えてください)
つぎに,停止するときは運動エネルギーがゼロで,ポテンシャルのみです.
するとこの2つの状態の間で,エネルギーは一定なので
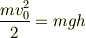
という式が立ちます.( 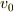 初速度,
初速度,  質量,
質量,  重力加速度
重力加速度 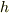 最高地点の高さ)
これを
最高地点の高さ)
これを 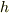 について解けば,それが答えです.
について解けば,それが答えです.
(もちろん運動方程式を解くこともできます)
Re: 斜面上の物体の運動
CO さんのレス (2005/09/26(Mon) 20:12)
> "どこまで上がれるか?"というのを"最高地点は?"と解釈して,変位x = 0とし
なぜこう考えたのでしょうか? 最高地点で速さが 0になる,の間違いではないでしょうか?
Re: 斜面上の物体の運動
リク さんのレス (2005/09/26(Mon) 21:09)
返信ありがとうございます.
渡邉さんへ 渡邉さんの解法でhについて解いたところ,答えは0.049となりました. プリントには解答がついていたんですが,解答は0.49でした.
COさんへ すいません,混乱していました. 斜面にそって物体を滑らせるので,x 成分だと思い,(重力はひとまず置いといて)どこまで上がれるか?ということは滑らなくなる・止まってしまう,つまり最高地点は?と思いました. 最高地点という言葉が思い浮かんだときに,自由落下の公式が出てきて,yをx , gをaと置き換えてx = 0としました.
問題文には物体の重さが書かれていないので,重さに関係する式は反射的に省きました. 何だか凄く意味不明な考えで解いてしまいました.
Re: 斜面上の物体の運動
渡邉 さんのレス (2005/09/26(Mon) 21:29)
そうですか.では,途中から放物運動をするのでしょうか.(高さ0.2m以降は,そのときの速度で,放物運動する事になります.答えが0.2mより大きければ,そのように考える必要がでると思います) よく考えてみてください.または,教科書を調べてみてください.僕の頃の教科書には載っていたと思います.(少なくとも問題集には・・・)
Re: 斜面上の物体の運動
RAMSTEIN さんのレス (2005/09/26(Mon) 22:15)
> a = g sinθより,a = 0.98m/s > > "どこまで上がれるか?"というのを"最高地点は?"と解釈して,変位x = 0と し, > x = vt + 1/2at^2に代入していくと > t = 0 ,0.49 > となります.
”最高地点は?”の解釈は,変位x=0だと ひょいと初速であげた最初の時間と,行ってじきに重力(傾斜があるから ちょっと弱めに)で戻って帰ってきたときの時間になってしまうと思います.
最高地点は,行って戻ってくる折り返し地点の速度が0になったとして解釈すると
v=v0 - gt 0=v0 - gt v0 = gt t = (v0/g)
で, 高さをhとして, h=v0t - (1/2)gt^2 に,このt=(v0/g)の時間をいれて計算してあげればよいかと.
gは,今回は傾斜sinθ=1/10(θ=90°で自然落下です)で,重力加速度を弱めにしてあげれば なんとかなるとおもいます.
けれどエネルギー保存則からも解いていけると思います.
あと,リクさんに質問なのですが,もしよろしかったら教えてください. 初速の向きと,重力加速度の向きはどんなふうに 自分のなかで意識して計算しますか? いつ符号の持つ意味を気にして計算式に入れていきますか?
以上です.
Re: 斜面上の物体の運動
yama さんのレス (2005/09/26(Mon) 22:23)
リクさんの答の0.049mというのは最高点の高さだと思いますが,斜面に沿って測った最高点までの距離はいくらになるか考えてみてください.
Re: 斜面上の物体の運動
tomo さんのレス (2005/09/26(Mon) 22:36)
リクさん,みなさん,こんばんは. tomoです.
> 渡邉さんの解法でhについて解いたところ,答えは0.049となりました. > プリントには解答がついていたんですが,解答は0.49でした.
これは,問題が求める解答にそっているかどうかの違いだけで, どちらも合っていると思います.
0.049は,地上からの高さ,0.49は斜面に沿って上がった距離ですね. 問題文で「斜面にそって上向きに滑らせた物体は」という記述があるので, おそらく斜面に沿った距離を聞いてきているのでしょう. ただ,「どこまで上がることができるか」と書いてあるので, 地上からの高さを答えても間違えではないと思います(が,試験では×かもしれません).
この問題では時間を聞かれていないので,等加速度運動の,
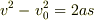 (
(  は最後の速度,
は最後の速度, 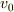 は初速度,
は初速度,  は加速度,
は加速度,  は変位)
という式が有効だと思います.最高地点では速度が
は変位)
という式が有効だと思います.最高地点では速度が  になることを考えれば,
になることを考えれば,
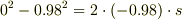 したがって,
したがって, 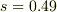 と求まります(斜面にそって上向きを正としています).
と求まります(斜面にそって上向きを正としています).
#1 リクさんの最初の書き込みで,「a = g sinθより,a = 0.98m/s」とありますが,
加速度の単位は ![[{\rm m/s}]](http://hooktail.maxwell.jp/bbslog/c768030579addce296532204d42fdb8c.png) ではなく
ではなく ![[{\rm m/s^2}]](http://hooktail.maxwell.jp/bbslog/5284f68ef8b5636b71bf387ab2c4d22f.png) なので,ご確認を.
もしかしたら2乗の書き方が分からなかっただけかもしれませんが・・・.
なので,ご確認を.
もしかしたら2乗の書き方が分からなかっただけかもしれませんが・・・.
#2 RAMSTEINさんもおっしゃっていますが,どちらを正にするかを, きちんと決める習慣をつけると良いと思いますよ.
#3 これも最初の書き込みで,「x = vt + 1/2at^2に代入していくと t = 0 ,0.49となります」
とありますが, 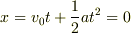 (
(  )を解くと,
)を解くと,
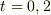 と求まると思います.
と求まると思います.
 の時に
の時に 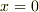 にいて,
にいて, 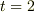 の時に
の時に 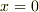 に戻ってくるという意味ですね.
直接,問題の解答には関係ないですが,一応.
に戻ってくるという意味ですね.
直接,問題の解答には関係ないですが,一応.
がんばってください :)
Re: 斜面上の物体の運動
渡邉 さんのレス (2005/09/26(Mon) 23:01)
こうなるとNo.6889に書いた内容がただの意地悪に見えてきますね・・・
ところで答えですが,ポーンと数値だけ書くのは好ましく無いと思います. どこまで上がるかの問いかけに対して 「初期位置から斜面に沿って0.49mだけの距離進んだところまで上る」 「初期位置の高さより0.049mだけ高い,斜面上の位置まで上る」 のいずれも正しい答えだと思います. (ただし上の答えは近似を使っています.)
僕なんかはそうやって,すましてきました.