強制振動

強制振動

Κ さんの書込 (2005/09/08(Thu) 02:26)

線形微分方程式を自分で勉強していたところ，非同次のときの特殊解は実際に代入したりして見つけろとありました．教科書に強制振動の特殊解の導き方が長々とかいてありましたが，テストのときは結果だけ覚えて使うのでしょうか？

Re: 強制振動

yama さんのレス (2005/09/08(Thu) 23:37)

特殊解を見つける方法として，まず未定係数法があります．特殊解を定数を含む式の形で予想して方程式に代入し，定数を決定するわけですが，どのような形の特殊解を予想すればよいかは，非同次項の形によって大体決まっているので，よく出てくる形については憶えておいたほうがいいでしょう． もっと一般的な方法としては定数変化法があります．特に摩擦がないときの強制振動の方程式は１階の方程式に帰着させることができるので，定数変化法が有効です．

Re: 強制振動

Κ さんのレス (2005/09/13(Tue) 23:30)

返信遅れてしまって申し訳ありません． 演習本を調べたところ，いきなりＸ＝〜とおく，っとあったので意味がわからなかったのですが，これが未定係数法のきまった形ということですね．この形だけを覚えればいいんですね． 僕が解いている問題は，減衰振動に強制力が働いている奴なのですが，それだともう一つの定数変化法は使えないのですか？

Re: 強制振動

ｙama さんのレス (2005/09/14(Wed) 09:33)

未定係数法については，その通りです．ただし，予想した式が一般解と一次独立でない場合は，定数が消えてしまって求まりません．その場合はその式に t または ｔ 2 をかけた式を仮定すればいいでしょう． 定数変化法は減衰振動に強制力がはたらく場合にも使えます．具体的な計算方法については，微分方程式の本に書かれていると思います．

Re: 強制振動

Κ さんのレス (2005/09/14(Wed) 12:03)

わかりました．調べてみます． もう一つ，減衰の一般解のことなのですが，線形微分方程式は 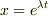x=e^{\lambda t} とおくと，必ず解けると書いてあったのですが，問題では 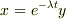x=e^{-\lambda t}y とおいて解いていました．要は，代入して求まればなんでもいいということだと思いますが，解法のテクニックかなんかでしょうか？僕は，余計面倒くさいと思ったのですが（積の微分とかでてきて）． どうでもいい質問ですみません．

Re: 強制振動

ｙama さんのレス (2005/09/14(Wed) 16:10)

x=e^{-\lambda t}y と置くのはおそらく \frac{dy}{dt} の係数が0になるように λ の値を定めるためだと思います．そうすれば ｙ については，減衰のない振動の方程式になるので，減衰のない場合の解を応用できるわけです．

もちろん 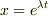x=e^{\lambda t} と置くほうが一般的だと思います．この場合は λ が一般には複素数になることに注意が必要です．

Re: 強制振動

Κ さんのレス (2005/09/15(Thu) 01:17)

λが複素数になったとき，オイラーの式を適用するとsinの係数にiが出てきますが，それは任意定数に含んでしまってもよいのでしょうか？ 結局，全部任意定数に含むなら一般的なやり方の方が早いですね．

Re: 強制振動

Κ さんのレス (2005/09/15(Thu) 01:27)

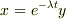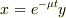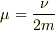すみません．間違いがあります． 問題では x=e^{-\lambda t}y とおいて解いていました．の部分は x=e^{-\mu t}y ただし \mu=\frac{\nu}{2m} νは抵抗の比例定数，ｍは質量です．申し訳ありません．

Re: 強制振動

ｙama さんのレス (2005/09/15(Thu) 08:39)

x=e^{-\lambda t}y と置いて \frac{dy}{dt} の係数が0になるように λ の値を定めると λ=μ になるので，初めから x=e^{-\mu t}y と置いても同じことです．いずれにしても y については減衰のない振動の方程式になります．

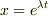x=e^{\lambda t} と置く場合は，積分定数も一般に複素数になるので，i を含めて任意定数としてもかまいません．

Re: 強制振動

Κ さんのレス (2005/09/15(Thu) 11:15)

ありがとうございました．レベルの低い質問ですみませんでした．