ベクトルの発散・回転について

ベクトルの発散・回転について

popo さんの書込 (2005/09/02(Fri) 23:13)

はじめまして!!宜しくお願い致します(^ ^)

学校でベクトルの発散や回転（div・rot）について習ったのですが 実際にはどういったところで使われているのですか??

【電磁気学】や【流体力学】などで使われているらしいのですが いまいちわかりにくいのでどなたか理解されている方や知っている方 具体的にはどういった感じで応用されているのかを教えて下さいm(- -)m

お願いします!

Re: ベクトルの発散・回転について

CO さんのレス (2005/09/03(Sat) 21:11)

こんにちは，popo さん．

ベクトルの発散や回転がどのように応用されているのかについては電磁気学や流体力学の教科書を見ればすぐにわかると思います．

それらを読むと，電磁気学ではマクスウェル方程式という基礎方程式そのものがベクトルの回転や発散を用いて表されていることに気づくでしょう．マクスウェル方程式は次のように書かれます．

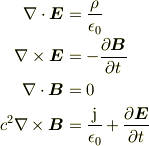
\nabla \cdot \bm{E} & = \frac{\rho}{\epsilon_0} \\\nabla \times \bm{E} & = -\frac{\partial \bm{B}}{\partial t} \\\nabla \cdot \bm{B} & = 0 \\c^2\nabla \times \bm{B} & = \frac{\mathrm{j}}{\epsilon_0} + \frac{\partial \bm{E}}{\partial t}

流体力学についても図書館や書店などで本をパラパラとめくってみると，どのように使われているのかわかると思いますよ．

Re: ベクトルの発散・回転について

にしかわさん さんのレス (2005/09/27(Tue) 14:50)

電磁気が応用される分野で，やはり計算が必要な場合，ie機器の設計などにおいて，上記マクスエル方程式を解くことはよくされます．

例えば，電力機器（中の電界分布）やアンテナや半導体の中の導波路など，電気工学から電子工学まで幅広く応用されます．

なんか薄っぺらい返答ですいません．

Re: ベクトルの発散・回転について

トミー さんのレス (2005/09/28(Wed) 01:11)

popoさん，はじめまして！トミーと言います．

学問的な応用は，かぎしっぽの方々が答えてくださるかと思うので，私は身近な事例を挙げて答えさせていただきます．少し長くなりますが…

今，目の前に四方八方に水を飛ばす，ほぼ点と見なすことができるくらい小さな噴水の口があると想像してください．地面に設置されていたりするのではありません．口だけが宙に浮いていると考えてくださいね．その口を覆うようにして，これまたすごく小さな立方体の箱を置いたとします．この箱も宙に浮いていることになります．仮にdiv<b>D</b>の<b>D</b>を，その噴水から湧き出る流水の速度とみたてると，div<b>D</b>は，その箱の表面を通って流れ出てくる単位時間当たりの水量を表していることになるのです．これが大まかな“発散”の考え方です．

では，なぜこれが電磁気学に応用されるかというと，先程仮想した「小さな噴水の口」を「正の点電荷」に置き換えてください．すると，電気力線が四方八方に伸びていきますよね？これを先程仮想した流水と見なし，この点電荷を覆うようにして小さな立方体を置くと，先程の噴水の時と全く同じ状態が作り上げられるのが分かると思います．だから，“発散”は電磁気学でも用いられるのです．

次に“回転”ですが，これは風見鶏を考えていただくと分かりやすいと思います．風力は大きさと向きを持つベクトルです．鶏の各部分に当たる風力が一様であれば，風見鶏は回転しませんが，それらに差があれば，回転を始めます．

発散と回転を用いた重要な公式に「ガウスの定理」と「ストークスの定理」があります．この二つの定理は電磁気学や電磁波工学において非常に重要なものとなっていますので，興味を持たれたら勉強されると良いと思います．