無題
無題
あさ さんの書込 (2005/08/31(Wed) 17:26)
こんにちは．なんか物理とは離れてしまうのですが，不定積分の積分定数の図形的な（＠原始関数をf(x)があったときの面積にする，よく積分の説明に使われる図というかグラフと言うか・・・・．）意味ってなんなんでしょうか？
Re: 無題
やかん さんのレス (2005/08/31(Wed) 18:50)
あささん，はじめまして！高校生の方ですか？とても面白い質問ですね．
私も学力は高校生（以下かも．年だけ食ってるけど）なので，
数学的にちゃんとしたお答えではない事をご了承いただきたいのですが
面積のゲタ（テストで成績が悪いときなど，ゲタをはかすとか言いますが）
と考えては如何でしょうか？つまり，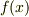 
のグラフを
真上に引っ張り上げると，高さは高くなり，面積は大きくなりますが，面積の変化率
（原始関数を微分したもの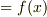 
）は隣同士の細い棒グラフとの差だから変わらないですよね．
Re: 無題
Joh さんのレス (2005/09/01(Thu) 04:32)
直感的に言うと，微分っていうのは，すごく細かい部分の傾きですよね．そこで，ある場所での傾きを調べて，ちょこっと線を伸ばして，またその場所で傾きを調べて，またちょこっと線を伸ばして，ってつなげていくのが積分です．(線が伸びてく動画を想像してみてください．)線をつなげた結果，ドラえもんが描けたとしましょう．しかし，計算で必要としたのは，微分だけでしたので，空間のどの位置にドラえもんが来るか（描き出す点をどこにするか）という不定要素があります．それが積分定数です．描き出す点を予め指定しておくのが定積分です．
以上，非常に乱暴で大雑把なイメージでした．
